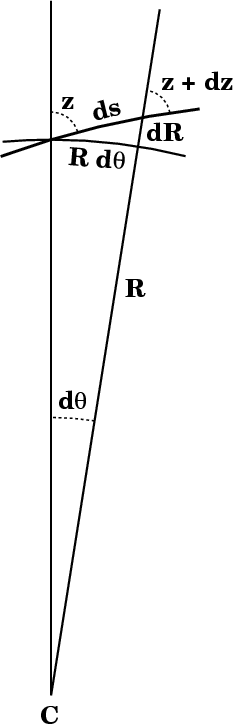
There's not much to it. Here's the differential triangle:

The element of path length ds along the ray corresponds to the increment dR in distance from the center of the Earth, at C. The local zenith distance at a distance R from the center is z; at R + dR, it's z + dz. But because the local vertical at the latter point has been rotated by dθ (the angle at the center of the Earth, between the two local verticals), the differential of refraction dr is not just dz, but
so that
From the little differential triangle, we see that
so
We will shortly need dR/R (see below), so let's rearrange this to give
Now, the refractive invariant is
which is a constant. So we can set its logarithmic differential equal to zero:
or
Now plug in the expression found earlier for dR/R, and use the fact that dθ = dr − dz:
or, cancelling the two dz terms,
so that
(Note that there is a minus sign because n decreases as R increases, going outward from the observer toward space.) This is the most useful form of the refraction differential. It shows how extremely sensitive the refraction is to the local zenith distance: where the ray is horizontal, (tan z) becomes infinite.
If you want to see how the integration is actually carried out, see the integration page, which contains plots of the integrand for several different zenith distances.
Copyright © 2003 – 2006, 2012 Andrew T. Young
or the
astronomical refraction page
or the
GF home page
or the Overview page