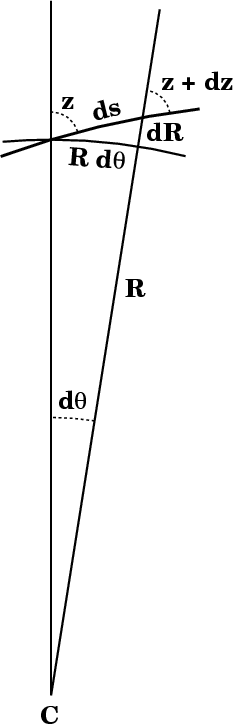
The differential of airmass is dM; it's just proportional to the
differential of path length ds in the figure, multiplied by the
local density, ρ.
Toward the end of his monumental work on Celestial Mechanics , Laplace has a long chapter dealing with atmospheric refraction. In the course of it, he derives a remarkable result, which seems to have been forgotten by most people today: the extinction of the atmosphere is related to its refraction. Those of us who remember Laplace's accomplishment sometimes call this result Laplace's extinction theorem.
The theorem is derived on pp. 283–285 of the fourth volume of the Mécanique Céleste, which you can download from the Gallica website. However, most readers will prefer to use the English translation by Nathaniel Bowditch, in which all the details Laplace elided with the facile phrase “it is easy to see …” are worked out in extensive footnotes. In Bowditch's translation, the equations are numbered; the extinction theorem appears as equation [8599]. (Yes, there really are that many equations, and more, in Laplace's work.)
In reading Laplace, either in the original or in Bowditch's translation, one must remember that he uses the notation of the emission theory in treating refraction, and that he employs the centesimal angular measures of the French revolution instead of the sexagesimal ones that are customary (still) today.
Laplace's obsolete terminology and notation present a considerable barrier to the modern reader. Therefore, it's useful to express the theorem in modern notation. Furthermore, one can give the matter a clearer and more succinct treatment today (see below).
Let's just state the theorem first, and then see where it comes from. Bowditch translates it in words as follows:
Therefore the logarithm of the intensity of light, of any heavenly body, is proportional to its refraction, divided by the cosine of its apparent altitude.
We must immediately notice that the proportionality constant is negative, because the stars become dimmer as they approach the horizon, and their refractions increase. Furthermore, one should strictly say the relation is a linear one, rather than a simple proportionality.
A modern astronomer would measure the light of a star on the logarithmic magnitude scale introduced by Norman Pogson in 1857. The magnitude m of an object is given by
where I is the intensity, and mzero-point is a term that absorbs the units and defines the “zero-point” of the magnitude scale. (Magnitudes can be regarded as negative logarithms to the base 2.512… .)
In terms of magnitudes, Laplace's result is equivalent to saying that the magnitude of a celestial object is a linear function of its refraction.
The law of atmospheric extinction, which was discovered by Bouguer and by Lambert around 1670, is that the logarithm of the transmitted intensity is a linear function of the mass of air in the line of sight. Expressed in magnitudes,
where M(z) is the relative airmass function (i.e., the relative amount of air in the line of sight, usually normalized to unity at the zenith), and m0 is the magnitude the object would have outside the atmosphere, at zero airmass. The parameter A is called the “extinction coefficient” by astronomers. (As the star grows fainter near the horizon, the stellar magnitude becomes numerically larger; therefore the extinction coefficient is a positive quantity.)
Strictly speaking, this “law” is true only for monochromatic light. In actual measurements, or even visual observations, some interval of the spectrum is involved. Within this range, different wavelengths have different extinction coefficients, and the simple linear relation given here is not accurate.
Finally, as the zenith distance z is the complement of the altitude, we can write sin z where Laplace and Bowditch have “the cosine of the altitude”. Then, if we use r for the refraction, Laplace's extinction theorem is succinctly expressed as
That is: the airmass is proportional to the refraction, divided by the sine of the apparent zenith distance of the object.
A very convenient corollary is: near the horizon, where z is nearly 90°, we have sin z = 1 (very nearly); so the extinction (in magnitudes) is very nearly proportional to the refraction. This result is very useful in understanding the brightness variations across both the setting Sun and the adjacent sky.
Now, let's see where this relation comes from. Rather than follow Laplace's rather tedious derivation, let's re-do it, using modern arguments. We must assume that the extinction is entirely due to the gaseous atmosphere; that is, we ignore the part of the extinction due to aerosols.
The differential of airmass is dM; it's just proportional to the
differential of path length ds in the figure, multiplied by the
local density, ρ.
The figure is borrowed from the page where the differential of refraction dr is derived. Now, however, let's regard the differential of refraction from a different point of view: dr must be equal to the ray curvature multiplied by the element of path length ds. The curvature, in turn, is proportional to the component of the atmospheric density gradient dρ/dh normal to the path of the ray. As the atmospheric model is horizontally stratified, its density gradient is a vector directed vertically — i.e., toward the zenith. The component of this gradient normal to the ray is just proportional to sin z. So
Now comes the weakest part of the argument. We need to assume the density gradient is proportional to the density itself. Laplace justifies this by saying (on p. 554 in Bowditch's translation):
Very near the horizon, the diminution of light depends, like the refraction, upon the constitution of the atmosphere. … But we may, without fear of any sensible error, use the hypothesis of a uniform temperature.
Actually, this is not as bad as it might seem: most of the refraction and extinction occur in the lowest levels of the atmosphere near the horizon, and the variation of temperature in these levels is small — just a few per cent. (The standard lapse rate of 6.5 K/km is about 2.2%/km.)
So we assume an exponential atmosphere, in which dρ/dh ∝ ρ, and have
But
If we eliminate the product ρ ds on the right side of the last proportionality for dr by replacing it with dM, we see that
Then integration will give Laplace's result, M ∝ r / (sin z), provided that we can factor some mean value of sin z out of the integrand when we integrate this differential relation.
In fact, this is not a bad approximation, because sin z is nearly constant through the atmosphere near the zenith (where z is nearly constant along the line of sight); and sin z is itself nearly constant near the horizon, because the sine function flattens out near unity when z is near 90°.
Notice that Laplace's result is trivially true for the flat-Earth approximation, where M = sec z and r ∝ tan z. Also, in a long duct, where the ray simply follows the curve of the Earth, and sin z is unity, the refraction in the duct is obviously proportional to the path length there.
The observational consequence of the extinction theorem at sunset is that abnormally large refraction is necessarily accompanied by abnormally large extinction and reddening. The first person to have noticed this seems to have been Robert Hooke. On p. 218 of his Micrographia, he says, of the Sun and Moon near the horizon:
… I have always mark'd that the more the limb is flatted or ovalled, the more red does the body appear, though not always the contrary.
(Of course, large refraction crowds more of the sky below the horizon into the narrow zone just above it, and so necessarily produces large flattening of the low Sun.)
Hooke's work is available on the Gallica website.
The great extinction that accompanies great refraction is particularly obvious in ducts. As they are (in practice) always of finite length, the setting Sun eventually is seen, very dim and very red, shining through the far end of the duct. A good example was published by Lehn and German in 1981.
There's a nice example of a sunset with a ducted mock mirage at Les Cowley's website. The lower image is inverted, so its top is the lower limb of the Sun, which is mashed down onto the duct in the upper solar image.
Copyright © 2003 – 2008 Andrew T. Young
introduction to extinction page
or the
GF home page
or the website overview page