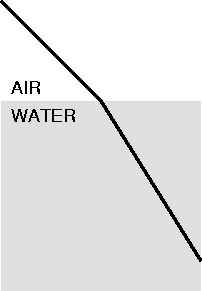
 <— water vs. glass —>
<— water vs. glass —>
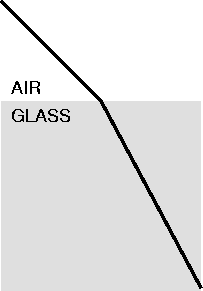
For thousands of years, people have noticed that a straight stick placed obliquely in water appears to be broken at an angle where it enters the water. This is the origin of the term “refraction,” which means literally “broken back.”
For about two thousand years, astronomers have known that heavenly bodies seen near the horizon appear slightly higher in the sky than they really are. This was attributed to refraction by the Earth's atmosphere; but it was not understood in detail until a couple of hundred years ago. This astronomical refraction, in its more extreme forms, is the cause of green flashes.
Refraction in the atmosphere is complicated by the continuous change in density of the air. So let's begin by considering refraction of light at a plane boundary between two uniform media — say, air and water, or air and glass. (For the moment, we will ignore the variations of density in the air.)
In the diagrams below, heavy lines represent “rays” of light. If you are not familiar with this conceptual fiction, please check the Optics for Beginners page before continuing here.
When a ray of light passes from one transparent material (say, air) into a different material (say, glass, or water), its direction changes; e.g.,
 <— water vs. glass —>
<— water vs. glass —>

The change in direction of the ray (represented by the heavy line in each diagram) is what is meant by the term refraction, which just means “bending” or “breaking.”
By the way, the diagrams here don't indicate which way the light is moving along the ray (from upper left to lower right, or from lower right to upper left). That's because the light follows the same path, no matter which way it goes. We often say “light rays are reversible” to summarize this property.
But the change in direction at the interface depends on the angle at which the ray meets the surface that separates the media. You can see from symmetry that if the ray is perpendicular to the surface on one side, it will still be perpendicular to the surface on the other; then there is no bending. As the rays become more oblique, the change in direction at the interface increases. So we need a quantitative description of the bending that separates the angular effects from the material properties.
The actual law of refraction was discovered in the early 1600s by a Dutch mathematician and geodesist, Willebrord Snel van Royen. (Because his name in Latin is “Snellius”, the law is often called “Snell's law” instead of “Snel's law”. You can find more information about Snel at the website of the Galileo Project. )
Snel found that there is a fixed ratio of two lengths in diagrams like those above. Let a ray of sunlight SR be incident on a rectangular tank of water, as shown below, where it is refracted at R. Extend the incident ray to A, on the vertical wall of the tank. Then the length of the actual refracted ray RC bears a fixed ratio to the extrapolated length RA, regardless of the angle of incidence.
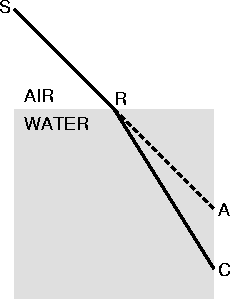
This ratio, RC/RA, is called the index of refraction, and denoted by the letter n. It is a property of the two media on either side of the refracting surface. For water and air, the ratio is very nearly 4/3; for glass and air, it is close to 3/2. (It's just a coincidence that the refractive indices of these common materials are so close to simple ratios; but it makes them easy to remember.)
It is convenient to assign every material an absolute value of the index of refraction, instead of dealing with a “relative index” that depends on the second material (air, in these examples). If we assign an absolute index of unity to vacuum, the index for air turns out to be nearly 1.0003 under ordinary conditions; then the absolute indices for most materials are very close to their relative indices, measured against air. So the index of refraction of water is about 1.33, and that of glass is about 1.5.
Of course, Snel's treatment of the problem is geometrical. If you know trigonometry, you can see that the ratio of the horizontal length RH to the diagonal RA is just the sine of the angle RAH, which is equal to the angle of incidence i measured from the line drawn perpendicular to the refracting surface at R. Likewise, the ratio RH/RC is just the sine of the angle of refraction RCH, or r . So Snel's ratio RC/RA is the same as (sin i )/(sin r ).
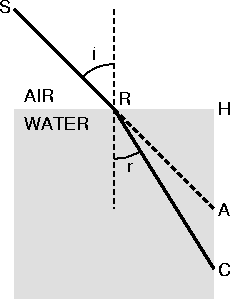
Consequently, the law of refraction is usually written as
these days, where n is the refractive index.
There is a nice interactive demonstration of the angular behavior of Snel's law in Fig. 3 on a commercial website. When you move the light source (at the right side of that diagram), pay particular attention to how quickly the ray in air moves when it is nearly horizontal, and the source is under water. This extreme sensitivity near grazing incidence is the key to understanding how small variations in the refractive index of air can produce the spectacular effects of mirages and green flashes.
This behavior near grazing incidence is so important for mirages and low-Sun phenomena that it deserves a closer look. Here's a plot of the angle in air against the angle in the water (both measured from the normal to the surface, remember; so grazing incidence means the angle in air is near 90°).
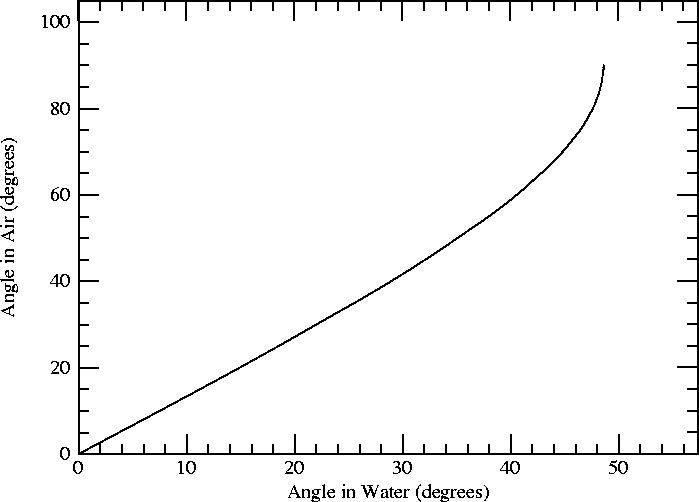
See that little hook at the upper right end of the curve? At the very
end, the curve becomes vertical; a tiny change in angle in the water
corresponds to a very appreciable change in the angle in air.
You might think that this wouldn't happen with the much smaller refraction of air (n = 1.0003) against vacuum (n = 1 exactly). After all, air is about a thousand times less dense than water, and the refractivity (n − 1) of air (0.0003) is about a thousand times less than that of water (0.33). But take a look (note that the scale is magnified somewhat compared to the plot above):
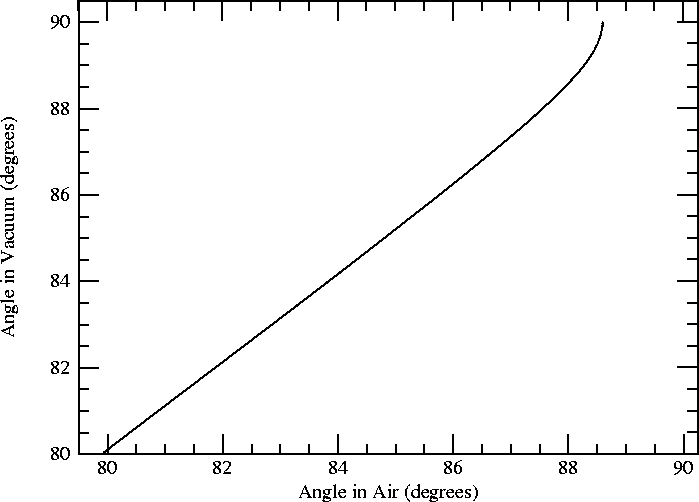
The curved part is only about half a degree here, as opposed to 10°
or so for water in the previous plot. But there's still a hook, and the
curve still becomes vertical at the end of it.
Why doesn't the size of these angular effects scale with refractivity? Well, remember that we are dealing with the sines of angles near 90°, which is the same as saying, “the cosines of angles near zero.” Those who have had calculus will recall that, for small angles x (in radians),
so that
Now, suppose we continue to put the angle i on the low-index side of the surface between the two media — i.e., in the vacuum in this case. Combine Snel's law
with i = 90° − x so that
and play the same game with r that we just did with i: if the deviation of r from 90° is y, then Snel's law becomes
where both x and y, the angles the rays make with the surface (instead of with its normal), are small. Now use the small-angle approximation discussed above, which gives
Now let the incident ray be grazing; that is, let x = 0. Then
But, as n differs from unity by less than 3 × 10−4, we may as well replace the factor of n on the left side by unity. Then, solving for y, we find
That means that, even for two layers of air whose temperatures differ by one degree, so that the difference in n is only 10−6, y is 1.4 × 10−3 radian, or about 4.2 minutes of arc — more than an eighth of the Sun's angular diameter. And, as the refraction at grazing incidence is proportional to the square root of the temperature difference of the layers, we see that even temperature differences of less than a tenth of a degree will produce refraction effects easily visible to the naked eye.
This shows why the small temperature differences between adjacent layers of air can have such obvious effects on the shape of the setting Sun, in spite of their very small differences in index of refraction.
On the other hand, these appreciable effects occur only very near the horizon, where the angle of incidence is really grazing. [More precisely, the term x2/2 must be small compared to (n−1) to get these large effects, so that it can be regarded as “negligible” and dropped, as we did above.] If the layers of air are very nearly horizontal, then only very nearly horizontal rays will experience these marked effects. That is why mirages and green flashes are observed only at (and below) the astronomical horizon: the rays have to be horizontal somewhere if they are to display these large effects.
All the discussion above deals with plane surfaces. But the Earth isn't flat! To deal with refraction in a curved atmosphere, we have to introduce some geometrical considerations, which have been put on a separate page.
Likewise, the atmosphere doesn't contain distinct, separate layers of different refractive index. Instead, the change of refractive index with height is both continuous and smooth. The ray bending produced by a continuous distribution of density is discussed on another page.
If you're not interested in the details of the calculation, but still want to know more about the refraction of astronomical objects by the atmosphere, see the page on astronomical refraction.
Copyright © 2002 – 2012, 2020, 2022 Andrew T. Young
Didn't find what you were looking for? Try the glossary or the alphabetical index.