Calculating Ray Bending

Introduction

I'll try to keep the treatment as simple as possible here, so a lot of refinements needed for an accurate calculation will be ignored. My aim is to show the basic physics, not to produce exact numbers. The accuracy of the results will be roughly 10%. (I'll also give the results of more accurate calculations for comparison.)

This kind of rough approximation is what one of my professors used to call a “bathtub calculation” — the sort of thing you can do in your head in the bathtub, without pencil and paper. (I'll actually not be quite that rough, so that the numerical results will be useful practical guides.)

By the way: if you're not familiar with the concepts of geometrical optics, I suggest you take a look at my introduction to optics page, before proceeding.

Basic facts

The density is important, because rays of light are bent toward the denser gas where the density changes from place to place. Air is densest near or at the surface of the Earth, and its refractivity  is very nearly proportional to the density.

The atmosphere is also curved, as it follows the shape of the Earth. In the calculations below, we'll adopt a rough value of 6400 km as the radius of curvature, to make the calculations simple. We'll also assume the density depends only on distance from the center of curvature — a pretty good assumption.

We'll measure temperatures in Celsius degrees, which are 9/5 the size of Fahrenheit degrees. Just a reminder: temperatures have to be measured from absolute zero, which is −273°C. That means a comfortable outdoor temperature of 25°C (77°F) is nearly 300 K, where the “K” means temperature on the absolute scale, named after Lord Kelvin; the Kelvin scale has degrees the same size as Celsius degrees, but starts at absolute zero instead of at the freezing point of water. I'll use 300 K as a typical temperature, even though it's a little warmer than average.

Straight lines?

Even if the air were isothermal (i.e., if it had the same temperature  everywhere), it wouldn't have the same density  everywhere, because it's in hydrostatic equilibrium: the air at each level in compressed by the weight of the air above it. The higher you go, the less compression; the density is lower at greater heights (which is why it's hard to breathe on mountaintops, and why jet airliners have to be pressurized.) So let's first figure out how to make the atmosphere (locally) homogeneous.

Obviously, if the density is decreasing upward because of the decreasing pressure, we can counteract this decrease by changing the temperature. In fact, the pressure falls off by about 1 part in 8000 for every meter of increase in height above sea level. We can compensate for this by decreasing the temperature by the same 1 part in 8000 for every meter of height. If the temperature is 300 K, we'll need a temperature decrease with height of 300°/8000 m, or .0375° per meter, to make up for the effect of decreasing pressure. If the temperature is colder than 300 K, a proportionately smaller lapse rate  will suffice.

(For comparison, Wegener (1918) calculates a value of 0.034°/m for 273 K; so the “bathtub” estimate is off by less than 10%, as promised above.)

Rays will be perfectly straight in a layer with this lapse rate ; but such a temperature gradient hardly ever occurs. It's over three times the adiabatic lapse rate (i.e., the gradient assumed by air in free convection), so this large drop in temperature with height can be maintained only near a warm surface. In models that reproduce inferior mirages over water, this value is reached only in the lowest 10 meters or so of the atmosphere.

An aside

You may have noticed, when I did the division a couple of paragraphs above, that a length of 8000 m somehow appeared in the denominator. This turns out to be the height the whole atmosphere would have if it had the same density throughout that it actually has at sea level. It's sometimes called “the height of the homogeneous atmosphere,” or the “scale height” of the atmosphere. (Radau calls it the reduced height  — a better name.) Although the real atmosphere actually extends much higher than this, it's a useful characteristic length to keep in mind.

Circulating rays

Note that a ray concentric with the surface of the Earth is not straight, but it is always “horizontal” — in contrast to the ray discussed in the previous section, which was really straight, and so could be horizontal at only one point. (See the figure below.)

Some people have worried about how to apply the refraction law to such a horizontal ray of light, because it does not cross any horizontal boundaries between denser and less-dense air in a stratified atmosphere. (In general, the curvature of the ray is different from the curvature of the Earth's surface; but here, we are only concerned with rays that bend just enough to follow the curve of the Earth.) The simplest solution to the “horizontal-ray paradox” is to remind ourselves that “rays” are an unrealistic mental construct: in reality, we always have a beam  of light; infinitely narrow “rays” don't really exist. So let's just apply Huygens's principle to such a beam:

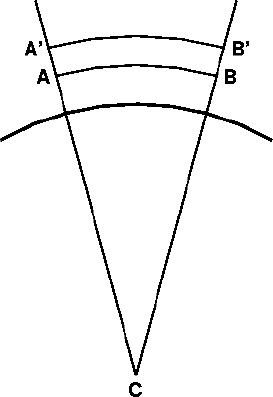In the figure at the left, the heavy arc denotes the surface of the Earth, with center at C, and the lighter arcs AB and A'B' concentric with it represent the sides of a beam of light propagating at constant height above the surface, from AA' to BB'. We can regard AA' and BB' as wavefronts of the (bending) horizontal beam at two different places; the direction of propagation is perpendicular to the wavefront. (Equivalently, we can say that the direction of propagation of a horizontal beam must always be perpendicular to the local vertical; the radial lines CAA' and CBB' radiating from the center of the Earth are the local verticals at A and B respectively.)

Evidently, to make the beam follow the Earth's curvature, its lower edge AB must travel more slowly than its upper edge A'B'. The speed of propagation is in fact just inversely proportional to the refractive index, n . As the distance to be traversed by our circulating beam is proportional to the distance R  from the center of the Earth, we require that 1/n  (which is proportional to the speed) be proportional to R ; or, in other words, we need the product nR  to be constant, independent of height above the Earth. (This will make the “optical path length” along AB the same as along A'B'.)

[If you find this argument too superficial to be convincing, you can go read the more rigorous derivations of the nR  = constant condition by Biot (1836), by Auer and Standish (2000), or one of the papers cited in my “horizontal-ray paradox” file, such as Bravais (1856) or Thomson (1872). There's also a wonderful mathematical treatment of circulating rays by Kummer (1860); a French interpretation of it by Verdet (1861) is available on Gallica; recently, Mila Zinkova noticed an English translation on the Web.]

To have nR  remain constant with height, n  must decrease by 1 part in 6.4 × 10⁶ for every meter of height, as R  = 6400 km = 6.4 × 10⁶ m. But the refractivity ( n  − 1 ) is only about 1/3200 of n ; so the density of the air [which is proportional to ( n  − 1 ), not to n ] must fall by about 3200/6.4 × 10⁶ m, or 1 part in 2000 for every meter.

Now, the decrease in density due to the decrease in pressure with height (1 part in 8000 per meter) is only 1/4 of this, so we need 3 times as much decrease from the temperature gradient, or 3 parts in 8000 per meter. That means the temperature must increase by 3 parts in 8000 of the 300 K, or about 900/8000 of a degree = 0.11° per meter. So a temperature inversion (i.e., increasing upward, instead of the usual decrease) of about 0.11°/m will produce a circulating beam or ray.

As a check, we can do the arithmetic a little differently. Because the refractive index n  decreases by 1 part in a million per degree, and we need a decrease in n  of 1 part in 6.4 million per meter, we would need about 1/6.4 of a degree per meter if the pressure stayed constant. But, as the pressure alone gives an effect equivalent to 3/80 of a degree per meter, we really need only ( 1/6.4 − 3/80 ); or, expressing the fractions as decimals, about 0.16 − 0.04 = 0.12°/m. (The lapse rate is, of course, the negative of this value.)

[For comparison, Wegener (1918) gives 0.114°/m as the critical temperature gradient; and J. de Graaff Hunter (1913) gives 0.066°F/foot, which corresponds to 0.116°C/m.]

Note that −0.12°/m is −120°/km, almost −20 times the lapse rate of 6.5K/km in the Standard Atmosphere . So the slight change of temperature with height in the Standard Atmosphere has hardly any effect on the ray curvature. This justifies, a posteriori , the neglect of temperature effects at the start of the arguments presented on this page.

Ray curvature in an arbitrary atmosphere

where we take γ to be positive if the temperature decreases with height, and a positive curvature means a ray concave toward the Earth.

Example 1: the Standard Atmosphere :

In the Standard Atmosphere, the lapse rate is 6.5°/km or  γ = 0.0065 K/m. The numerator of the formula above becomes .034 − .0065 = .0275, so the ratio k  is about 1/5.6 or 0.179. In other words, the ray curvature is not quite 18% that of the Earth; the radius of curvature of the ray is about 5.6 times the Earth's radius.

Example 2: free convection:

In free convection, the (adiabatic) lapse rate is about 10.6°/km or  γ = 0.0106 K/m. The numerator of the formula above becomes .034 − .0106 = .0234, so the ratio k  is about 1/6.6 or 0.152. In other words, the ray curvature is about 15% that of the Earth; the radius of curvature of the ray is about 6.6 times the Earth's radius. This is close to the condition of the atmosphere near the ground in the middle of the day, when most surveying is done; the value calculated is close to the values found in practical survey work.

Bear in mind that these values apply only near sea level. At appreciable elevations, the density of the air is less, so the ray curvature is also less. Likewise, these estimates are for sea-level temperatures near 300 K; in cold places, the density of the air is greater, and so is the ray curvature. And remember that these curvature estimates apply only to rays that are horizontal, or nearly so.

Note: You might have noticed that these values around 1/6 are about the fraction by which the setting Sun is flattened at the horizon. This is not a coincidence; these two quantities are in fact equal, as can easily be shown.

Historical note

The method used here to find the ratio of curvatures of the ray and the Earth is essentially the argument employed by Thomas Young in 1821. He also obtained a ratio of 5.6, as in the first example above.

Copyright © 2002 – 2009, 2012, 2016, 2018, 2020 Andrew T. Young

Didn't find what you were looking for? Try the glossary or the alphabetical index.

or the astronomical refraction page

or the GF home page