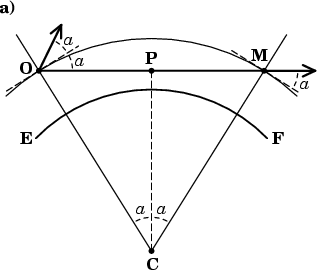
Here's a diagram showing the situation without refraction.
The surface of the Earth is shown by the heavy arc EF
with center at C.
An observer at O looks in the directions indicated by the arrows,
at angular altitudes a
symmetrically placed
above and below the astronomical horizon.
The local horizons at O and M are shown with short dashed lines
through those points.
The lower ray, OPM, is symmetrical about its lowest point, P.
You can see from elementary geometry that the dip a of the lower line of sight OPM is the same as the angle OCP at the center of the Earth, because both are complements of the angle COP. So the angle OCM at the center of the Earth, subtended by the arc between the observer at O and the point M where the lower ray re-crosses the observer's (curved) level surface, is 2a. And that's the same as the angle between the upper and lower rays at the observer.
The ray OPM below the observer's horizon has the same altitude a at M as its dip at the observer; so whatever refraction it might have above eye level (to the right of M) is the same as that of the ray above the horizon at O. In fact, the whole course of the lower ray to the right of M has exactly the same shape as the upper ray has to the right of O, because both rays have the same altitude at the same height above the surface of the Earth. So, no matter what refraction these rays suffer above eye level, their angular separation outside the atmosphere is the same as their angular separation at the observer, namely, 2a. Consequently, the sky at the horizon is not distorted: the magnification is unity.
As an aside, I note that Cassini's uniform atmosphere is a model of this kind. Consequently, his model produces unit magnification at the astronomical horizon, and very little distortion of the setting Sun.
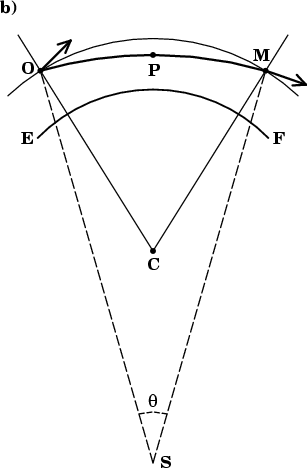Now let the ray OPM be bent by refraction.
If we keep O and M fixed, bending the ray moves P up,
so the dip of the lower ray at the observer becomes smaller.
The altitude and dip of the two rays at the observer have a new magnitude
b, smaller than the previous value, a ;
the upper and lower rays are now separated by an angle
2b at the observer.
These angles are very small — a few minutes of arc — so the curved ray OPM is well approximated by an arc of a circle; let S be the center of that arc. Then its central angle θ is also the change in direction of the bent ray within the layer below the observer (because the ray is perpendicular to the dashed radii OS and MS, at O and M, respectively). So the ray separation 2b at the observer is less than the value of 2a we had without refraction by just this bending, θ; that is, 2b = (2a − θ). Notice that θ is the contribution to the refraction of the lower ray made by the air below eye level.
But on every level surface above the observer (including the top of the atmosphere), the two rays are still separated by 2a, the angle between the local verticals at O and M (because both rays make the same angle, b, with their local horizons). Therefore the angular magnification of a small celestial object at the astronomical horizon is just
i.e., the ratio of the apparent to the true angular separation of the rays.
It is most convenient to write the angular magnification m in terms of the ratio of curvatures k of the ray and the Earth, which we found on the bending page. As the curvature is just the reciprocal of the radius of curvature, k = OC/OS.
Now, the length of the curved ray OPM is very nearly the same as the arc length OM measured along a level surface. But (using the fact that the arc length is just the angle in radians times the radius of the circle) OM = 2a × OC ; and similarly, OPM = θ × OS. If we equate these two expressions for the distance from O to M, we have
Sometimes it's convenient to work with the reciprocal K of the ratio k ; then m = (K + 1)/K.
On the bending page, we found that k is usually about 1/6 (which means K is about 6). This value makes m = 5/6, which is a typical value for the ratio of vertical and horizontal diameters of the setting Sun. (See the simulation of a sunset in the Standard Atmosphere, for comparison.)
However, when the observer is in a thermal inversion, the value of k can be much larger — approaching, or even exceeding, unity. What does this do to the flattening?
As k → 1, m → 0. That means the Sun flattens down into a thin line at the horizon. This condition is always seen from just above a duct. However, such strong inversions are usually accompanied by complex thermal structures that make it difficult to assign a well-defined flattening to the observed images.
When k exceeds unity, the observer is inside a duct. Then the Sun cannot be seen at the astronomical horizon, which is blocked by Wegener's blank strip.
As each value of m corresponds to a value of k, and each value of k corresponds to a particular lapse rate just below eye level, the observed flattening of the Sun at the horizon provides a good estimate of the lapse rate near eye level.
Copyright © 2006 – 2009, 2012 Andrew T. Young
Didn't find what you were looking for? Try the glossary or the alphabetical index.
or the
astronomical refraction page
or the GF home page