If you aren't too far above the base of the inversion that produces a mock-mirage flash — say, no more that a couple of dozen meters — the flash is thick enough to see with the naked eye. Yet you're usually in the inversion yourself; and Biot's magnification theorem means the local temperature gradient should compress images at the astronomical horizon. So, why is the mirage as thick as it is?
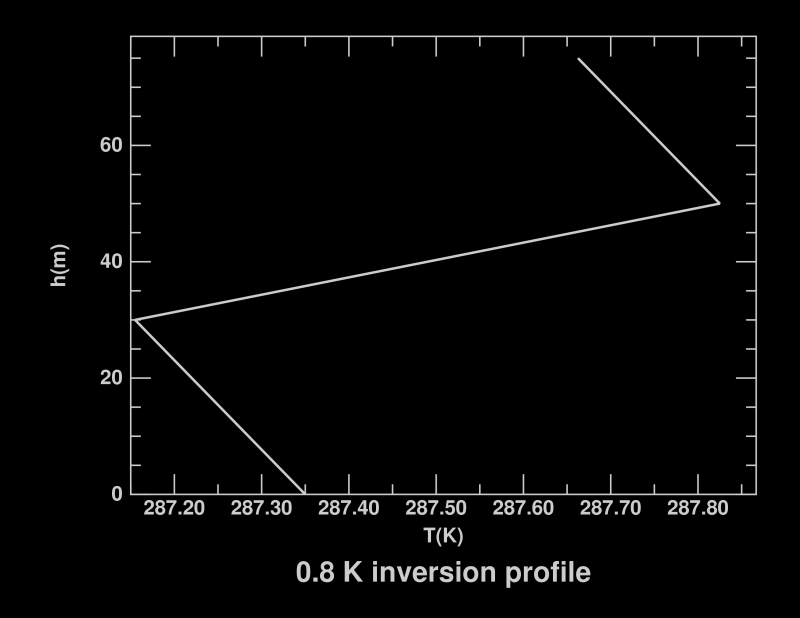
This is doubly puzzling if you try computing the image from a simple piecewise-linear temperature profile, like this one:
What you get is an extremely thin flash, like this:
Just to make this super-thin flash visible at all, I've had to double the normal resolution: each pixel in this image is just 3.75 seconds of arc across. This doesn't look at all realistic.
What's wrong? Well, as explained
elsewhere,
real temperature profiles can't have sharp corners.
So let's round off the corner, by smoothing it with a Gaussian of 1-meter
halfwidth. We get an appreciable mock-mirage flash, which looks much more
normal:
And if we smooth it with a Gaussian of 2-meter
halfwidth, we get quite a nice flash, like this:
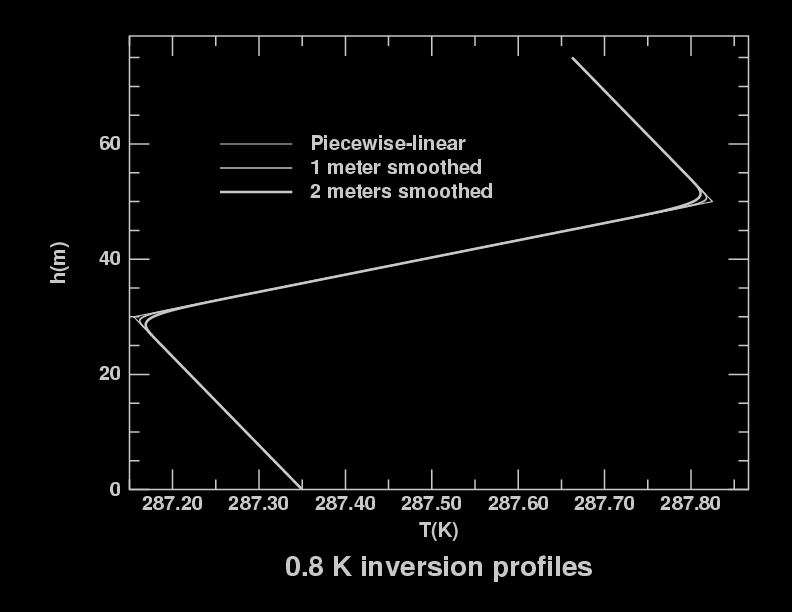You might think all this smoothing would make as spectacular a difference
in the temperature profiles as it does in the images. Here are the
three profiles together:
You can see the differences at the corners; but they're small. And they're even smaller when you look at the temperature scales — the biggest difference, right at the corner, is only 0.02256 degree!
How can less than one 44th of a degree make such a big difference in the appearance of the setting Sun? The answer is that it's the slopes of the temperature profiles that largely determine image displacements in the sky. That is, the important thing is the local lapse rate, and how it changes. Rounding off the corner makes a huge change in the lapse rate there, even though the actual temperature itself hasn't changed much.
Copyright © 2005, 2006 Andrew T. Young
or the
main simulation page
or the website overview page