The magnification at the astronomical horizon depends only on the density gradient just below eye level (which, for practical purposes, depends only on the temperature gradient). This page is devoted to demonstrating the truth of this statement.
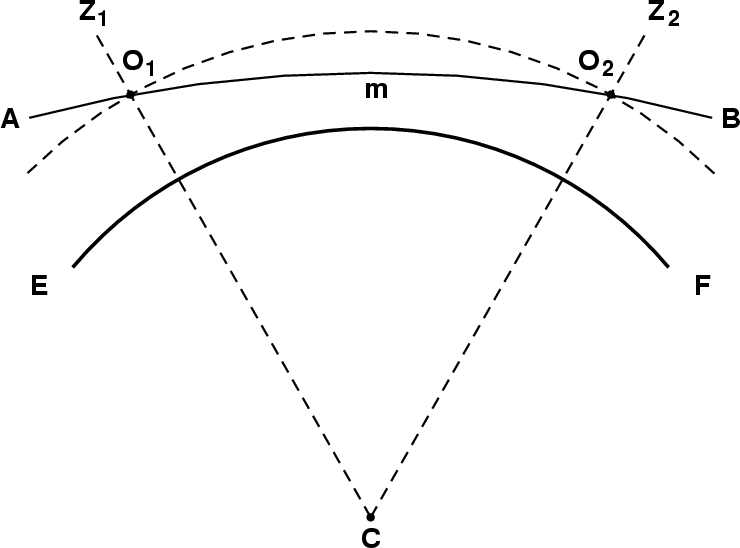
Suppose, following Wegener, we divide the atmosphere into two parts: the part above the observer, and the part below. In the diagram, we have two observers, O1 and O2 at the same height above the surface of the Earth EF, centered at C. The dashed arc passes through the observers, and is a horizontal surface. The zenith of observer O1 is in the direction CO1Z1, and that of observer O2 is in the direction CO2Z2.

The thin solid arc AB represents a ray of light from some distant celestial object; it is symmetrical about its lowest point, m. This ray makes the same angle with the horizontal at both observers. If we suppose the object is off to the right, beyond B, observer 1 sees it below the astronomical horizon, while observer 2 sees it an equal angle above the horizon.
The apparent zenith distance of the object, as seen from O2, is the angle Z2O2B; its apparent altitude, h , is the complement of this angle (i.e., the acute angle at O2 between the solid ray and the dashed horizontal surface). At O1, the apparent altitude is just −h . But the true zenith distances of the same object at the two observers differ by just the angle Z1CZ2 at C between their zenith directions. This central angle depends on the ray curvature between the two observers' positions, which in turn depends only on the density gradient (which means, for practical purposes, the temperature gradient) between the height of the observers and the height, m, of the lowest point on the ray.
So, if the observer moves along the dashed horizontal surface, at constant height, the true altitude of a fixed star changes by the amount of this central angle, while the apparent altitude changes by an amount that depends on the temperature gradient just below eye level. The ratio of the changes in apparent and true altitudes is the average magnification between the altitudes h and −h . If the angles are small, m approaches the height of the observer, and as h approaches zero, the ratio approaches the magnification at the horizon.
Perhaps this will be clearer if you think in terms of one observer and two objects, symmetrically disposed about the astronomical horizon, at apparent altitudes h and −h . The ray path for each object is exactly the ray path AmB shown in the diagram above; imagine making two copies of this diagram, and pivoting one with respect to the other about the center C until the two observers' positions coincide. Then, if you enlarge the part of the diagram around the observer, you have something that looks like this:
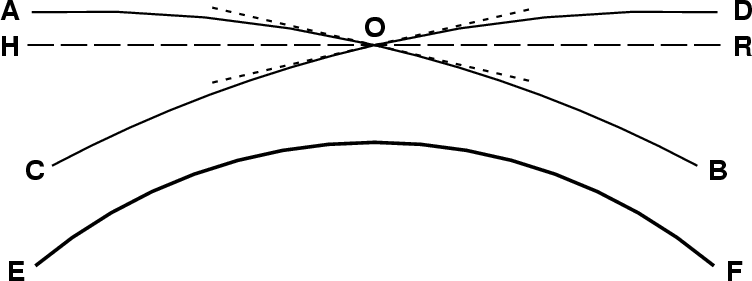
Now, instead of one object and two observers, we have one observer and two objects; call the objects B and D. The plane HOR is the plane of the observer's astronomical horizon. The two rays AOB and COD have the same shape, but are mirror images, reflected about the vertical through O. You can see that the short dotted lines that are tangents to the two (solid) rays at O make equal angles with the local horizontal; the objects B and D have equal altitudes, apart from sign.
As in the previous diagram, the true altitudes of B and D differ only by the central angle between the points where a ray crosses the observer's level; and this depends only on the temperature gradient below eye level. Clearly, the magnification is the ratio of the difference in apparent altitudes (2h ) to that central angle.
The exact relation can be derived just by using basic geometry. However, we'll use a little calculus in the section below.
The apparent altitude ha is just the sum of the true altitude ht and the refraction, r:
And the magnification is the derivative
Unfortunately, we can only calculate r as a function of ha, not as a function of ht. So we write
and differentiate with respect to ha :
Then we can write
This allows us to calculate the magnification Mag from the slope of the refraction at the horizon.
Because the refraction gradient at the horizon is closely related to the magnification, deriving a formula for the former is tantamount to deriving the latter (cf. the last two equations of the section above.)
The first person to have derived the magnification at the horizon seems to have been Kramp (1799). He assumed an exponential atmosphere, equivalent to adopting a constant temperature throughout; this gave him the wrong density gradient, and hence the wrong refraction gradient. Kramp noticed the discrepancy with observations, but was unable to account for it properly.
Biot (1836) was the next person to derive the gradient. He clearly understood the role of the temperature gradient. After first pointing out that the refraction out to a zenith distance of about 74° depends only on the state of the air at the observer, so that “the refraction is sensibly independent of the actual state of the distant layers,” he notes that
. . . what has not been noticed [is that] there exists near the horizon, or rather at the horizon itself, an analogous theorem, which has, moreover, the singularity of always being true, in all possible atmospheric conditions, not just approximately, like that which we have mentioned, but in an absolute and rigorous manner.
. . . But, just as, near the zenith, the [refraction gradient] depends only on the refractivity observable in the layer where the observer is found, its value at the horizon depends at once on this and on its immediate decrease [with height]; such that the action of distant layers has absolutely no influence. …
Besides the unexpected singularity of finding an element of the horizontal refraction, independent of the state of distant layers, and of obtaining it, in all possible cases, without integration; besides the relation which results between the increase of the refraction near the horizon and the equally observable variations of refractivity in the lower layer, the theorem which I shall state would have still other useful applications.
As one such application, he mentions the ability to decide whether a refraction table has been calculated from a particular model atmosphere, and in this way deduces that Newton's refraction table, whose origin had been obscure, was in fact based on an isothermal (i.e., exponential) model.
Clearly, Biot was the first person to understand the importance of these relationships. I think Biot deserves credit for (in effect) discovering the magnification theorem, though he did not apply it to the magnification of celestial objects at the astronomical horizon himself.
Copyright © 2002 – 2003, 2005, 2006, 2012, 2021 Andrew T. Young
or the symmetry page
or the GF home page