Making realistic simulations is more difficult than making the simple cartoons used in the gif animations. The primary requirement is to determine the actual color stimulus at each point in the image. The CIE established a standard method for doing that in 1931; but it requires knowing the spectral radiance throughout the image. But, as Dietze showed, green flashes are nearly monochromatic; so we must have their spectral radiances in considerable detail.
Given the spectral radiance of a point in the image, we need the integrals of its products with three color-matching functions, which are tabulated at regular intervals of wavelength. The conventional way of evaluating these integrals is to approximate them numerically (as described in my tutorial note on color science). That means we need a table of the spectral radiance for each point on the image.
The natural way to do this is to construct a monochromatic image for each of the tabulated wavelengths. At each wavelength, we calculate a refraction table, and use it to determine where on (or off) the Sun each point in the field of view falls. To obtain realistic results, we should include solar limb darkening, atmospheric extinction, and foreground sky brightness in the spectral radiance calculation. Each of these steps requires quite a bit of computational work.
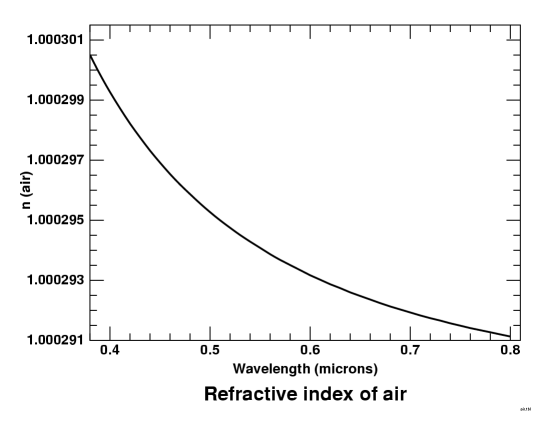Unfortunately, it turns out that the conventional method of doing the
spectral integrations (as a sum of terms equally spaced in wavelength)
is not efficient. The
reason is that the atmospheric dispersion curve (shown at the left here)
is very steep at short wavelengths, and very flat at long ones.
The great dispersion at short wavelengths means that the monochromatic images must be very closely spaced there, to avoid obvious artifacts (such as discontinuities in the colored composite images). If we have a resolution of, say, ten seconds of arc in the image, we don't want the atmospheric refraction anywhere to vary more than a second or two from one wavelength to the next. But this requires such close wavelength spacing at the blue end of the spectrum that we have to use hundreds of monochromatic images to cover the whole visible spectrum, if equal steps in wavelength are used.
One could imagine transforming the wavelength scale in a nonlinear way, so as to make the monochromatic samples equally spaced in refractive index. But then another problem arises: we have to transform either the power spectral density of the solar spectrum (i.e., the solar spectral radiances), or the weights used to represent the CIE color-matching functions, to compensate for this unequal spacing. That's pretty drastic.
However, there is a simpler treatment that accomplishes almost the same result. If you look at the refractivity formulae that have been proposed for air, you'll see that the leading non-constant term is roughly inversely proportional to the square of the wavelength. Now, as I point out elsewhere in these pages, a factor inversely proportional to wavelength squared is exactly what's required to convert spectral radiance as a function of wavelength to spectral radiance as a function of frequency. So you might expect that plotting refractivity as a function of frequency instead of wavelength would largely straighten out the dispersion curve. And sure enough, it does.
Furthermore, it's easy to tell MODTRAN to tabular solar spectral irradiances as functions of frequency, rather than wavelength. (MODTRAN conveniently takes care of both the solar spectrum and the atmospheric transmission for us.)
However, MODTRAN is not the answer to all of our problems here. For one thing, it doesn't calculate refraction very accurately. And its small number of atmospheric levels prevents it from calculating refraction for the complicated atmospheric models needed to generate accurate simulations of mirages: I often have to use thousands, or even tens of thousands, of layers in the refraction calculation.
Fortunately, there is a way around this limitation. Some years ago, I found a good interpolating function to represent the Forbes effect (the curvature of the Bouguer-Langley plot for heterochromatic radiation). So, given several (airmass, transmission) pairs, it's possible to fit this fudge-function to these values, and produce a simple analytic formula for the transmission at any other airmass. (It's been tested extensively on MODTRAN output, and provides an excellent representation of broadband transmission; see
A.T.Young, E.F.Milone, C.R.Stagg
On Improving IR Photometric Passbands
Astron. Astrophys. Suppl. 105, 259–279 (1994)
for examples.)
In particular, the formula provides a realistic representation of the declining effective extinction coefficient at very large airmasses, and so can safely be used for extrapolation to large arguments. This is particularly important here, because near-critical refraction leads to much larger airmass values than MODTRAN can generate.
So I fit my function to the MODTRAN airmass-transmission (or, actually, airmass-irradiance) values near the horizon in each spectral interval, save the coefficients in DATA statements, and then use these tabulated values to calculate the solar irradiance for each monochromatic image, no matter how big the accurate value of airmass turns out to be.
This trick allows me to calculate only (!) 33 actual refraction (and airmass) tables, and interpolate the rest of the points in the spectrum. I actually divide the frequency interval between 12500 cm-1 (800 nm wavelength) and 25000 cm-1 (400 nm) into 100-cm-1 intervals, so there are 126 terms in the sums that represent the integrals. So the problem is large, but manageable.
Of course, this still requires interpolating the ordinates of the CIE color-matching functions to the centers of the 100-cm-1 intervals. But this can easily be done once, and saved in a DATA statement.
Likewise, the limb-darkening coefficients — which are tabulated at round values of wavelength — have to be interpolated to the midpoints of the integration intervals.
This brings up a point that often causes trouble: the distinction between radiance and irradiance. What we need for the image is the solar radiance (often called “surface brightness”), which is conserved in passing through lossless optical systems. But MODTRAN provides the solar irradiance (the total amount of transmitted light from the Sun). We have to scale the irradiance spectrum by the ratio of central to average disk brightness to get the relative radiance spectrum at the center of the disk, and then apply the limb-darkening function to get the relative radiance of each pixel in the solar image.
I emphasize this matter, because many people are confused by the radiance/irradiance distinction. It has also caused some confusion in the mirage literature, where people who didn't understand the distinction thought that refraction in mirages could cause changes in radiance (or its visual analogue, luminance ) of images simply by defocusing or focusing the light; it can't.
If you are one of the victims of this confusion, I suggest a look at Chapter 8 of Warren Smith's Modern Optical Engineering , 3rd edition (pp. 225–230). He very clearly explains that even astigmatic systems (like the atmosphere) can't violate this basic principle, which is related to the Second Law of Thermodynamics (sometimes it also goes by the name of the Lagrange Invariant , or the Helmholtz reciprocity principle , in optics). See also the section on Brightness in my JOSA paper on visual effects in green flashes.
There is also some useful treatment of this matter on the Web here. Unfortunately, many textbooks muddle the issue by introducing an imaginary “Lambertian surface”, which is not something that exists in the real world; it is a creature of elementary physics textbooks, like the frictionless cart, the massless string, and the inertialess pulley. We would be better off without this chimera.
The main practical problem is the enormous space taken up by the image arrays. To store 126 monochromatic images, each of which may contain several million pixels of 4-byte floating-point values, is a killer for some desktop systems (I only had 256 MB of memory on my machine at home, and 128 MB on the older one at work, when I first did this work).
Right off, I save some space by storing only half of each image, because they're symmetrical. And, although the sky should occupy several image columns on either side of the Sun, it's reasonable to save just a single column of sky and duplicate it repeatedly in the final image (as I'm not trying to model the solar aureole in great detail here).
A subtler problem is the question of subscript ordering. The natural way to calculate everything is a row at a time: the extinction and sky brightness, for example, can be taken as constant along a row of the image. So the row-index of each array ought to come last (as that varies most slowly in Fortran arrays). And, as the natural way to work is to scan right across a row, the column-index of each array ought to come first (as that varies most rapidly in Fortran arrays).
But what about the index that represents the wavelength or frequency at which each monochromatic image is calculated? The obvious way to do things would be to put the row- and column-indices next to each other, and the wavenumber index last. But that turns out to produce disk thrashing: the image elements are so widely separated in memory that the arrays are continually being swapped out to the hard disk. So it takes forever.
Furthermore, when we build the monochromatic images, we're scanning the columns and rows of each one at a fixed point in the spectrum; but when we use them to calculate the CIE integrals, we have to sit at a fixed point in the image and scan through the whole spectrum. So there isn't an obvious way to optimize the use of subscripts here.
If the columns have to come first and the rows have to be last, the only place for the wavenumber index is in the middle. This produces a rather strange-looking subscript combination, but it works.
This takes care of the major problems: the solar radiance spectrum, the limb darkening, and extinction by the molecular atmosphere. However, the sky brightness and aerosol extinction still have to be added.
At first glance, one would be inclined to let MODTRAN handle this. After all, it contains a sophisticated aerosol model, and can calculate sky brightnesses. But then I'd have to re-run hundreds of MODTRAN cases to re-generate the interpolating coefficients every time I chose a new aerosol case.
Worse, the interpolating function only works well when the airmass is a good measure of the absorbing species responsible for the extinction. It doesn't work very well when the extinction is dominated by non-uniformly-mixed species, like water vapor and aerosols (both of which are concentrated toward the surface of the Earth).
This isn't a severe problem for water, because where the water absorbs enough to spoil the fit, the absorption bands are nearly black anyway, and contribute little to the observed radiance. But it's really a problem for the aerosol, which causes both a marked extinction gradient near the horizon, and the sky brightness near the Sun. And the aerosol is very non-uniformly mixed, as it's strongly concentrated toward the Earth's surface.
So I decided to let MODTRAN handle just the molecular atmosphere, and ran it with zero aerosol throughout. That means I have to treat aerosol effects separately. That, in turn, means I have to choose a model for the vertical distribution of the aerosol scattering.
Clearly, it's impractical to treat the aerosol in as much detail as MODTRAN does. So I decided to model the aerosol as if it had an exponentially decreasing mixing ratio with the gas. This means I can just calculate an effective aerosol “airmass” factor by multiplying the actual airmass integrand by a simple declining exponential function of height above the surface, at each point. The rate of decline is set by a sort of aerosol scale height, which is really the aerosol mixing-ratio scale height, not the absolute aerosol density scale height.
However, this means I have to re-run the refraction model (yes, for all 33 wavelengths) every time I choose a new aerosol scale height. That often requires several minutes of machine time. But it's better than having to do hundreds of MODTRAN runs. And, on the other hand, I can change the amount of aerosol without having to re-run the refraction/airmass/aerosol-mass calculation.
The only other item required to calculate aerosol extinction is its wavelength dependence. This is well known to be nearly inversely proportional to wavelength. Rather than adopt a detailed power-law function of wavelength, I'm using a simple 1/λ scaling, which is probably good enough here.
The aureole is considerably more messy. Although MODTRAN calculates sky brightnesses, it does so using a low-order expansion of the aerosol's angular scattering (the so-called single-scattering phase function).
That works well over most of the sky. But it breaks down in the aureole (the bright patch of sky around the Sun): to get accurate results there, studies have shown that over 100 terms must be used in the spherical-harmonic expansion of the phase function. This is another machine-buster; forget it.
Worse yet, the programs that are available for this calculation assume a plane-parallel atmosphere without refraction — restrictions that are completely invalid at sunset, where curvature effects are extremely important. So far as I know, nobody even knows how to calculate the aureole radiance at the horizon realistically (let alone efficiently). And besides, I don't care about the brightness distribution over the whole sky; I just need a little bit around the Sun itself.
So I adopt a rather ad hoc model for the aureole, based on two simple ideas. First, the aerosol is almost completely forward-scattered light. If I look no more than a degree away from the Sun, the light hasn't been scattered by more than a degree; so the airmass it has passed through is almost identical to that of the directly-transmitted solar image. (See, for example, p. 164 of the English translation of G. V. Rozenberg's monograph, Twilight .) That allows a simple calculation of the attenuation of the aureole light.
Second, the forward-scattering lobe of the aerosol phase function is mainly due to the “diffraction peak” in the scattering. It's well known that the scattering cross-section of a particle is twice its geometric cross-section. For particles larger than the wavelength, half of the scattering is due to light geometrically transmitted through the particle, where refraction sends it all over the sky; and the other half of the scattering is in the diffraction peak, concentrated in the forward direction. The angular width of the peak is roughly the ratio of wavelength to particle size.
Most of the aerosol extinction is due to particles comparable to the wavelength, which send the light all over the sky; they don't contribute much to the aureole. So the aureole light — that is, the sky brightness near the Sun — must be due to scattering by the few particles that are much larger than average.
I now offer the following arm-waving argument: Let's simplify the aureole scattering by saying that the half of the aerosol optical depth that's not in the peak sends light all over the sky, and is effectively lost to the aureole. The other half of the scattering goes into the aureole, where it gets attenuated by general atmospheric extinction just like the direct solar image.
If the aerosols produced only forward scattering, all the light they remove from the direct beam would reappear in the aureole, slightly changed in direction. Then there would be no aerosol attenuation of the aureole light -- only the direct solar image would be reduced in brightness by the aerosol scattering. (Of course, the molecular atmosphere still attenuates the aureole; but that's taken care of by the MODTRAN calculation.)
Actually, only half of the scattering by large particles is in the (forward) diffraction peak. Then the other half of the scattering cross-section represents light lost from the aureole. So that half of the aerosol optical depth would be effective in attenuating the aerosol brightness, in addition to the molecular attenuation.
This gives us the aureole irradiance . But what we need is its radiance . To get that, we spread the total aureole light over an area of sky several times larger than the Sun. If the aureole is (say) 6 degrees across, its effective diameter is 1/10 of a radian. But the Sun's diameter is only 1/100 of a radian; so the aureole irradiance is spread over a hundred times the solid angle of the Sun.
So we need a sort of “dilution fudge-factor” to allow for the size of the aureole. This will scale the aureole radiance down compared to the average solar radiance. It turns out that factors on the order of 0.01 do indeed produce realistic-looking sky brightnesses; so the semi-quantitative argument offered here seems to preserve enough of the physics to be useful. (I do not argue that it is very accurate.)
We still have to take the Sun's altitude into account. The average path of aureole light observed at some altitude is intermediate between the path from the eye to the center of the Sun, and an unscattered (but refracted) ray traced backward in the direction of observation. Let's assume that picking an airmass halfway between these will give a reasonable estimate of the aureole in that direction. So, compute the airmass for the mean altitude:
alt.for typical path = (alt.for direction observed + alt.of Sun)/2.
This has a problem when the Sun is below the horizon; then we have no way to connect geometric solar depression with airmass, which is the argument needed for the irradiance formula.
One way around this is to assume airmass is proportional to bending (Laplace's extinction theorem). But how to estimate "bending" beyond the end of the refraction table, where we have no refraction value? A crude estimate is
total bending = (refraction at apparent horizon) + (solar depression below its true depression at apparent horizon).
airmass = (airmass at app.hor.) * (total bending) / (refraction at app.hor.)
for the airmass of the Sun, in computing the mean airmass for the aureole.
Unfortunately, this produces unrealistic images when the aerosol scale height is small and its optical depth is moderate. The use of only half the total aerosol optical depth to attenuate the aureole lets the Sun shine through plainly when the line-of-sight optical depth is fairly large, even though we know it should disappear in the haze.
The reason is that the line-of-sight transmission is now very small, so that the transmitted solar image is — in reality — very faint. In the real world, this dim solar image is drowned out by multiply-scattered light in the optically thick haze at the horizon. But the model so far considers only single scattering, and so ignores this component. However, the importance of multiple scattering in the aureole near the horizon was established some 30 years ago by McPeters and Green [Appl. Opt. 15, 2457–2463 (1976).]
A very crude allowance for this multiply-scattered light can be made by including some second-order scattering. The illumination of the haze at the horizon is mainly from the blue sky; but the haze is strongly forward-scattering, so the lower parts of the sky are most effective.
I arbitrarily assume the light source corresponds to the sky about a quarter of a radian above the Sun. That makes the effective airmass of the light source about 4. The scattering in this part of the sky is mainly Rayleigh scattering, so the light source for the second scattering roughly corresponds to the light from the 4-airmass molecular atmosphere, taking account of the Rayleigh optical depth there.
We can easily calculate the monochromatic optical depth in this part of the sky for pure Rayleigh scattering. The transmission is exp (−Mτ), where M is the airmass and τ is the optical depth in the zenith (about 0.1 at 500 nm wavelength, and inversely proportional to λ4.) The scattered fraction is just 1 minus the transmission.
The solar-irradiance formula for this part of the sky, multiplied by the scattered fraction, gives the scattered irradiance . Rayleigh scattering is nearly isotropic; so divide by 4π steradians to get the blue-sky radiance . This is the light source for the second (aerosol) scattering.
Now the radiance of the re-scattered light can be found. This time we just use the full optical depth of the aerosol along the line of sight: the transmission of its optical depth is again 1 minus the scattering, so we find the scattered radiance. This has to be added to the aureole to get the total airlight in the direction of observation.
A little attention also has to be given to the airlight below the apparent horizon. The sea is practically black; but the optical depth between its surface and the observer contributes second-scattered diffuse light. If we don't allow for that, we get very unrealistic-looking black seas, even when there's a lot of aerosol.
Once we have computed the sky brightness at a given altitude in the image, it just gets added to every pixel at that altitude (including those occupied by the solar image, don't forget).
When I first tried doing all this, I found the solar limbs were infested with “jaggies” — aliasing artifacts. So it was necessary to introduce a little do-it-yourself anti-aliasing to shade off the average pixel radiances gradually when the limb fell inside a pixel.
In principle, this is easy, because the Sun is (in real space) circular. You know the position and slope of the limb accurately; it's just a matter of finding what fraction of the pixel's area is inside it.
In practice, it's a little tricky, because a square pixel in image space projects to a rectangular one in object space, where the Sun is. The algorithm for determining the shading fraction also has to account for the change of limb darkening between the corner of the pixel nearest the solar center and the very limb itself. I don't wish to bore you with these tedious details; but it's necessary to point out that this problem has to be dealt with, if some reader wants to try this game at home.
Having done everything above for each quasi-monochromatic image, there's the matter of summing up the products of the monochromatic radiances and the color-matching functions at each image point to obtain CIE XYZ values, and then converting to sRGB space, as described on the spectrum-rendering page.
For examples of how this turns out, see the array of images showing the effects of different amounts and distributions of haze.
This all works well for inferior-mirage flashes, where the green flash itself
is the only part of the Sun's disk that's visible. But when any part of
the disk but the limb is visible, it's so much brighter than the flash
that the latter is not very conspicuous, as you see here in the
mock-mirage flash at the
left. There just isn't enough dynamic range in a computer display to show
the extremes of brightness in a real sunset, where there's so much more
red light than green.
You can try to make the reds dimmer by making the haze layer shallow, which makes things near the horizon darker. But that doesn't help enough. In this example, seen from a height of 38 m, the haze scale height was set to 40 m; but — although this dims the part of the Sun near the horizon quite considerably — it still leaves the top of the Sun much brighter than the mock-mirage flash. This approach doesn't work because the flash isn't far enough above the red disk. If you make the reddening haze dense enough to dim the top of the disk, it dims the flash even more; and the diffuse light at the horizon starts to drown it out, too.
So it's necessary to compress the dynamic range somehow. A natural approach is to do something like what color film does: let the reds saturate when they're too bright. Although this distorts the colors, making the red-orange setting Sun turn orange or even yellow, it at least produces a result that's distorted in the same way color photographs are distorted.
The image at the right shows what you get when you do that. The
brightnesses have been increased by about a factor of 2.7, and the reds
that should have have data values around 690 have been held to 255.
This turns the top of the disk orange (just as a slightly over-exposed
photograph does), and of course flattens the limb-darkening. But at least
the green flash now has a more natural appearance.
Incidentally, these examples show why mock-mirage flashes are so seldom noticed by visual observers: without some magnification, the flash is lost in the glare of the Sun's disk. (The images shown here have a resolution of 7.5 seconds of arc per pixel — about 8 times the resolution of the unaided eye — so they show details visible to an observer using 8× binoculars.)
© 2005 – 2007, 2012, 2021, 2023 Andrew T. Young
Back to the GF home page