Astronomical Coordinates

Introduction

It may be useful to explain the basis of astronomical coordinates for readers who are unfamiliar with them. There is also a need to clarify the distinction between these angular coordinates and ordinary “rectangular” three-dimensional spatial coordinates, which requires more discussion than is suited to the Glossary .

This was brought to my attention by a reader who noticed that the Glossary's entries for the different kinds of “horizon” were vague and needed more details. The oversight was mine; I was so familiar with these terms that I had not noticed the subtle differences that require careful treatment. This page is an effort to fill the gap.

Places and directions

Astronomers and other technical workers distinguish the astronomical horizon from the apparent horizon , and from other kinds of horizons (such as the geometric horizon ). In addition, the place where the Earth and sky meet is sometimes treated as a physical location on the Earth, and sometimes as just the direction in which an observer sees it.

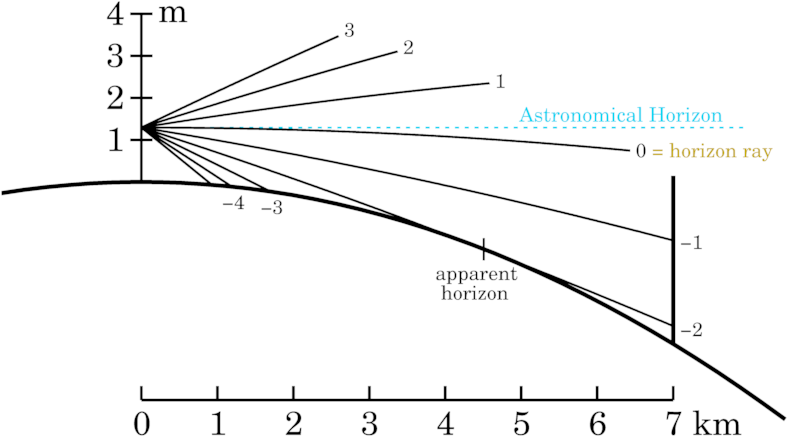
These different concepts are usually not explicitly distinguished, leaving the reader to resolve the ambiguity from context. Specialists can usually infer what's meant, but the average person can be left confused. To understand the differences, consider the ray diagram below.

The plane of the diagram is perpendicular to the Earth's surface. The heavy solid arc represents the curved surface of the Earth. Thinner curved lines are refracted rays that meet the eye of an observer about 1.3 meters above the surface. The number at the right end of each ray is its angular altitude at the observer, in minutes of arc. [The vertical target 7 km from the observer will not be discussed here.]

Horizon rays diagram

The rays converge at the observer's eye, on the left. The dotted blue line is the intersection of the observer's astronomical horizon with the plane of the diagram. The ray marked 0 at its right end is only horizontal at the observer's eye , so it is tangent there to the plane of the astronomical horizon.

Because the observer is above the surface, a zone of sky 2 arc minutes wide is visible below  the astronomical horizon. This strip of sky appears to meet the surface at the apparent horizon. The most distant surface point seen by the observer is about 4½ km from the observer, and is marked by a small vertical tick where the ray touches the surface. Because the apparent horizon is 2 arc minutes below the astronomical horizon, this angle is called the dip of the [apparent] horizon. Usually the word “apparent” is omitted when discussing dip.

If the observer is at sea, or on dry land overlooking the ocean or a large lake, the most distant visible point will be somewhere on the surface of the water. Then the apparent horizon is usually called a sea horizon. The position of the most distant point on the sea is not well defined, because it depends on the difference of the curvatures of the surface and the ray, both of which are very small. Here are some illustrative numbers:

The figure has a vertical exaggeration of over 550 times, to separate the rays on your screen. The vertical scale of the diagram makes the width of the surface arc nearly half a meter. At the places (near 3½ and 5½ km from the observer) where the arcs for the surface and the apparent-horizon ray are barely separated in the figure, the mid-lines of these arcs would be only 7½ cm apart. This is much smaller than wave heights on large lakes; swells on the ocean are still larger. In the real world, the most distant point at the apparent horizon could be the highest wave crest anywhere between 3 and 6 km from the observer.

These numbers depend on the ray curvature, which depends on the density gradient of the air near the surface, and changes with the weather, the time of day, and the time of year.

Two or three dimensions?

If the dimension of distance is so uncertain, why use it?

The term “apparent horizon” can denote either the position of the most distant visible point (tick mark), or the direction of the ray from the observer to that point. Usually the context allows the reader to infer what is meant. But, as we just saw, the computed distance is unreliable; so it's common to ignore distances entirely, and just deal with directions.

When distances are so uncertain as to be useless, or so huge as to be practically infinite, we can omit them.

Spherical coordinates in astronomy

We can separate distances from directions by using spherical coordinates. The diagram above shows two rectangular coordinates: a vertical one (the scale of height in meters at the observer's position), and a horizontal one (the scale of kilometers at the bottom). These can be replaced by moving the origin to the observer's position, and adopting a spherical coordinate system centered there. (Spherical coordinates are the 3-dimensional extension of polar coordinates to 2 dimensions.)

A direction in space can be defined by two angles, if distances are ignored. This means we are moving from a 3-dimensional (x,y,z) description of space to a 2-dimensional one. That 2-D space is the surface of a sphere, and the coordinates that we use are called spherical coordinates. In astronomy, the sphere is called the celestial sphere.

The celestial sphere is often regarded as having infinite radius, so that parallel lines (which all have the same direction) meet the sphere at the same point. The observer is at the center of the celestial sphere; so a point on the celestial sphere is a direction in space.

The horizon system

The astronomical horizon is the plane perpendicular to the direction of gravity at the observer. The direction vertically above the observer is the zenith; the opposite direction (straight down) is the nadir. In practice, the astronomical horizon is a plane tangent to a pool of still liquid — usually liquid mercury — at the observer's position. This plane meets the celestial sphere in a great circle: the astronomical horizon.

If the astronomical horizon is not hidden by the terrestrial features that define the apparent horizon, the entire upper hemisphere of the celestial sphere is visible. The angular elevation of an object in the sky above the astronomical horizon is the altitude of the object, measured positively upward. (The altitude of the zenith is +90°; the altitude of the nadir is −90°.) At sea, only apparent altitudes (measured above the visible sea horizon) can be observed directly; these have to be corrected for dip of the sea horizon before they can be used for navigation.

The astronomical horizon is inaccessible to most people, who live in or near cities that are in river valleys surrounded by hills. For them, the astronomical horizon is hidden by the apparent horizon, which blocks their view of astronomical objects near rising and setting. Geodesists and astrometrists have instruments that allow them to determine where the astronomical horizon is, by relating the gravity field to optical measurements.

More technical jargon

On a sphere, any two points that are not 180° apart define a great circle. The circles on the celestial sphere that pass through both the zenith and nadir are called vertical circles. Two vertical circles are important; the one that passes through the celestial poles is the meridian, and the one perpendicular to the meridian is the prime vertical. (The celestial poles are the two points in the sky that do not participate in the daily apparent rotation of the sky.) The intersections of these two vertical circles with the astronomical horizon are the cardinal points (N, S, E, W).

(Here's a diagram of the basic relationships, provided by Wikimedia Commons.)

An important rule is: The altitude of the North Celestial Pole is the (astronomical) latitude of the observer. However, the apparent altitude must first be corrected for refraction for this to be accurate. The “pole star” Polaris  is close to, but not at, the north celestial pole.

The altitude of an object is measured along the vertical circle that passes through the object. The second angular coordinate in the horizon system, called azimuth, is the angle between the object's vertical circle and the meridian. It is usually measured positive to the East from the North point, though other conventions are sometimes used by surveyors and other workers.

Other kinds of horizons

If there were no refracting atmosphere, the rays would be straight and not curved. In imagining such a situation, it's common to consider the dip of a distant surface point as seen (by a camera) from some elevated observing position. As the ray-tracing involves only simple geometry, this apparent horizon is often called the geometric horizon. This is sometimes done when introducing the topic of dip (for example, here).

Various specialized fields have also used their own terminology. A geodesist has mentioned a geodetic horizon, referring to the geoid rather than the actual surface of the Earth. Geologists (mainly stratigraphers) have their own special uses of “horizon”.

At one time, there were attempts to split hairs, and to distinguish between the ordinary astronomical horizon (as a particular plane at the observer) and a parallel plane through the center of the Earth. This introduced the terms “rational horizon” and “sensible horizon”. The latter gained common use in the literature of navigation, but has not been used by astronomers in the past century, except occasionally in historical articles. It led to confusion with the “visible” horizon.

Thanks

Thanks to Dan Freund, who pointed out the need for this page.

Back to the . . .
GF reading page

or the GF pictures page

or the main mirage page

or the GF home page

or the website overview page