When we observe sunset and mirage phenomena, we're usually standing on the surface of the Earth. But standing on the surface doesn't mean our eyes are at the surface. Even at sea, if your eyes were at the surface of the water, your nose would be under it; this isn't a tenable position for very long.
Diagrams in textbooks are often drawn as if the observer is at the surface of the Earth — partly because the height of the eye is very small compared to the size of the Earth: a person's eyes are about 1.6 meters above the ground, but the radius of the Earth is over 6 million meters. But, in this case, “very small” isn't the same as “negligible.” Let's work it out:
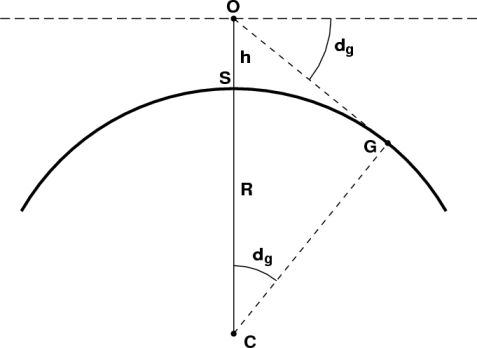
Here's a diagram of the situation without atmospheric refraction. The diagram shows a vertical plane through the center of the Earth (at C) and the observer (at O). The radius of the Earth is R, and the observer's eye is a height h above the point S on the surface. (Of course, the height of the eye, and consequently the distance to the horizon, is greatly exaggerated in this diagram.) The observer's astronomical horizon is the dashed line through O, perpendicular to the Earth's radius OC. Because we are temporarily assuming that there is no refraction, the observer's apparent horizon coincides with the geometric horizon, indicated by the dashed line OG, tangent to the surface of the Earth.

Because of the observer's height h, the apparent horizon lies below the astronomical one by the angle dg, which is the geometric dip of the (unrefracted) horizon.
Because the tangent OG is perpendicular to the radius CG of the circle that represents the Earth, the angle OCG is also equal to the dip dg, because both angles labelled dg are complementary to the angle COG. So we can apply elementary trigonometry to calculate the dip:
But h is, as remarked above, very small compared to R. That means the dip angle itself is small; so we can apply the small-angle approximation cos x = 1 − x2/2 to the left side of the equation, and use the binomial theorem to expand the right side [after dividing both numerator and denominator by R, to get 1/(1 + h/R)], which becomes 1 − h/R. Then the 1's cancel, leaving us with the approximate result
To get some feeling for how this works, look at some numbers. Suppose you're standing at the edge of the sea, with your toes at the waterline. Your eyes are about 1.5 meters above the sea, and R = 6.4 × 106 m. Then sqrt(3/6.4 × 106) is about 0.00068 radians, or 0.039°, or about two and a third minutes of arc.
As the resolution of the normal eye in broad daylight is about one minute of arc, this dip is an easily visible angle. So, although the angle is small, it is hardly negligible, even for a naked-eye observer standing at the water's edge. Clearly, dip is an appreciable effect for all real-world observations.
Before considering a more realistic situation that includes refraction, notice that the dip is the same as the angle OCG at the center of the Earth. A rule of thumb is that a minute of arc on the surface of the Earth is a (nautical) mile. So this calculation also supplies the distance to the apparent horizon: about 2 ⅓ nautical miles, in this example. Equivalently, we can say that as the (geocentric) angular distance to the horizon is sqrt (2h/R), the linear distance to the horizon is R times this, or sqrt (2hR).
So far, we have ignored refraction, and drawn the line of sight to the apparent horizon as the straight line OG. But, in the real world, there is some terrestrial refraction between the observer and the horizon; the line of sight to the apparent horizon is not straight, but curved. So let's try to allow for that curvature:
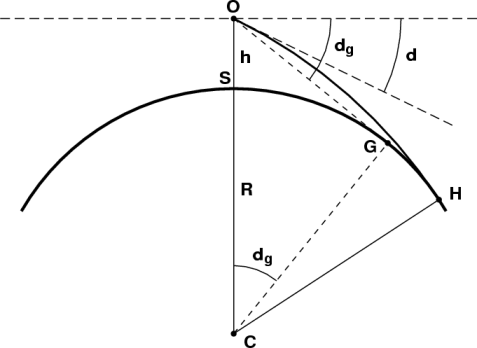
Usually, the ray is concave toward the Earth, as shown in this drawing. The solid arc OH now represents the curved line of sight; H is the (refracted) apparent horizon. Notice that refraction lets us see somewhat farther; but the refracted dip d between the horizontal (dashed) and the tangent to the curved line of sight is now less. So we no longer have the nice equality between the dip and the distance to the apparent horizon — although the refraction correction is usually small, so the geometric relationship is often roughly correct.
The derivation including refraction is a little tedious for a Web page, so I'll just quote the result here. If we can regard the ray OH as an arc of a circle, with a curvature k times the Earth's curvature (that is, the radius of curvature of the ray is R/k), then the above result is still true if we just replace R in the original expressions (without refraction) with R/(1 − k). This is equivalent to saying that the effective curvature of the Earth is simply diminished by the curvature of the ray: the Earth's curvature is 1/R, the ray's curvature is k/R, and the difference of the curvatures is (1 − k)/R.
In other words, everything is the same with refraction as it would be on a fictitious planet with a radius of R/(1 − k) and no refraction. So, as long as k is much smaller than 1. the numbers aren't greatly changed by refraction.
Clearly, both the dip and the distance to the horizon are still proportional to sqrt (h), but the proportionality constant depends on the value of k adopted — which is equivalent to assuming a particular lapse rate between the eye and the surface, as the ray bending depends mainly on this temperature gradient. Typical values used in practice are dip = 1.75′ × sqrt (h, meters) [taken from the Explanatory Supplement], and horizon range = 3.83 km × sqrt (h, meters).
On the other hand, when there is a strong temperature inversion, k can reach, or exceed, unity. The case k = 1 corresponds to horizontal rays that orbit the Earth indefinitely (a situation considered in exquisite detail by Kummer.) Values larger than 1 correspond to ducting conditions; if the observer is inside the duct, a pseudo-horizon appears above the astronomical one, so the dip of this apparent horizon is negative — a remarkable phenomenon that really is observed, occasionally.
On the other hand, the distance to the horizon is sensitive to the intervening thermal structure. Variations in lapse rate between eye and surface tend to make the distance to the apparent horizon appreciably larger than the simplistic argument above would suggest. And that means that it's common to see objects that are beyond the limit of visibility calculated from the Standard Atmosphere's refraction — especially if there's an offshore breeze that blows hot air from the land out over cold water.
Furthermore, the air temperature near the perigee point on the horizon ray is considerably closer to the temperature at eye level than is the temperature of the actual surface. That's because the Earth's surface isn't smooth: on land, your line of sight is usually intercepted by plants and structures well above the ground surface; and at sea, the apparent horizon is at a wave crest, well above the mean surface of the water. So it's difficult to know what temperature to use for the lowest point along the horizon ray. The effect is large for observers near sea level: raising the air temperature 1°C is nearly equivalent to raising the eye by 9 meters (about 30 feet). (See here for more details.)
Even so, it's fair to say that the dip is increased when inferior mirages are present, and decreased (or even negative) when thermal inversions occur, with or without mirages.
You can see some examples of dip variations in the green-flash pictures taken by Oscar Medina from his home at Pacific Beach, which have vanished from the live Web but are available up to about 2014 at the Wayback Machine. (The best examples are near the bottom of his Web page.) Several of his pictures show the roof of a large building nearly level with the sea horizon. In the ones having an inferior-mirage flash, the sea horizon is very nearly even with the top of the building. These flashes require water warmer than the air. But those with mock-mirage flashes, which are produced by thermal inversions below eye level, and hence require water considerably colder than the air at eye level, show a visibly higher sea horizon.
Another good picture of thermal effects on dip is shown on Les Cowley's website. There, an inferior mirage formed on top of a sunlit sea wall depresses the apparent horizon well below the normal sea horizon beyond it, making an illusory depression in the surface of the sea.
These effects are readily visible to the naked eye, and are quite striking to anyone who regularly observes sunsets from a place that has a suitable architectural feature nearly at the sea horizon. They were observed about 1889 by Annibale Riccò with the naked eye; but instrumental observations were first made by Laval (1707), who found variations of several minutes of arc. Later observations were made by Alexander von Humboldt, who first connected the dip variations with the changes in sea-surface temperature.
Without doing the arithmetic, it's hard to realize how big the dip is for an eye near sea level, and how long it takes for the Earth's rotation to change the Sun's altitude by a few minutes of arc. The diurnal motion takes 4 seconds of time to move 1 minute of arc in hour angle, so even at the Earth's equator, the Sun takes 4 seconds to move one arc minute with respect to the horizon. (At higher latitudes, the motion is oblique to the horizon, so it takes even longer to sink by one minute of arc; the time is larger by a factor that depends on the Sun's declination, but usually exceeds the secant of the latitude.) But the eye of an observer standing at the water line is about 1.6 meters above sea level, and so sees the sea horizon depressed by more than 2 minutes of arc. It takes the Sun at least 8 seconds to reach this depressed apparent horizon.
In 1997, Brad Smith inadvertently performed this experiment, thinking that his wife sitting on a beach in Hawaii had missed a sunset green flash. You can read his account of this in Sky & Telescope 93, No. 5, pp. 111–112 (May, 1997).
Similarly, Captain Egbertus Havinga reported that “Usually I observed from the lower bridge, the 2nd Officer on watch from the upper: when the sun set directly forward, I went and stood next to him. In the first case I saw the green flash a few seconds earlier”. These observers were about 10 meters above the water.
Likewise, in his book, on p. 59 of the Dover edition, Minnaert says:
Once, by running up the slope of a dyke, 6 yards high, I was able to watch the green ray for 20 seconds . . . .but in the original Dutch, the height was 6 meters, not 6 yards. With average refraction, the dip of the sea horizon there is over 4 arc minutes, which would delay the sunset about 16 seconds at the equator, and about 25 seconds at Minnaert's latitude in Holland. Remember that the exact value depends on the temperature difference between the eye and the wave crests.
Such observations are easy to make, given a clear view of the sea from a place not too high above it. The calculated delay between two heights will probably agree better with observation in the open ocean than observations from land, because the latter may be strongly influenced by unusual refraction in coastal locations, especially when the wind blows offshore. But, unless an observer is in a duct, the observation from the lower height will always see the sunset first, because the Earth is round, not flat.
Copyright © 2003 – 2013, 2020, 2025 Andrew T. Young
or the
main mirage page
or the GF home page