First of all, it's a mistake to call anything “the ” Standard Atmosphere, because many such artificial models have borne that name. What they all have in common is a tropospheric lapse rate of exactly 6.5°C per kilometer, and a temperature of 15°C at sea level. These arbitrary parameters were prescribed in 1919, and have remained fixed ever since then. It was originally intended for comparing the performances of airplanes with supercharged engines, and was also used to predict the trajectories of artillery shells and bombs dropped from airplanes; no one considered applying it to atmospheric optics.
From the start, this was supposed to be a sort of average of the few measurements of atmospheric structure available, ignoring the diurnal and seasonal changes in the real atmosphere. It was enthusiastically adopted by the aviation community as a reference model for calibrating barometric altimeters, and the meteorologists used it to estimate the heights of sounding balloons. As information about the upper atmosphere grew, the Standard Atmosphere was extended to greater heights; as better values for relevant physical constants and the Earth's gravity field improved, various defining constants in the standard models changed. So today there are several conflicting sets of Tables, each supposed to be the Standard Atmosphere.
Unfortunately, astronomers and geodesists were misled by the word Standard into thinking that the atmosphere could really be close to this artificial model, which resembles 18th- and 19th-Century mathematical models used in calculating refraction. But the real atmosphere varies with the weather, and cannot physically have a constant lapse rate.
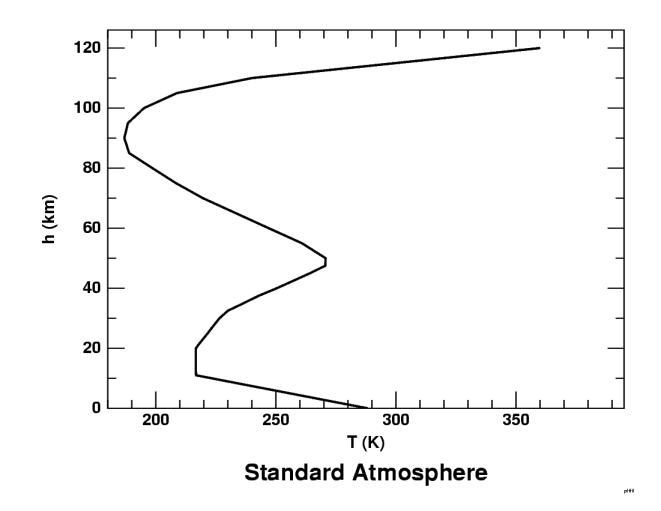
Here's the temperature profile for the 1976 version of the United States Standard Atmosphere. If you're a physics or math type, you may be momentarily confused by the layout of the axes: though height is normally considered the independent variable, it's plotted on the vertical axis here. It's standard practice in the atmospheric sciences to make the height axis vertical, so we'll use that convention.

The part of most interest here is the lowest section, where the lapse rate is 6.5 K/km. This is supposed to be an average value throughout the bottom 11 km of the atmosphere, where daytime convection stirs things up.
But this is only about 2/3 of the dry adiabatic lapse rate, which is what we'd have if the atmosphere were free of water vapor and thoroughly stirred. A considerable part of the discrepancy is due to the release of latent heat as warm, humid air is convected from the lower levels to higher ones: when the air cools to the point where condensation of water vapor into cloud droplets occurs, the latent heat is released to become “sensible heat”. If the cloud becomes dense enough to rain out, much of the heat that was released remains in the upper air.
Often, the convective columns overshoot during the day, and the air subsides after sunset, warming the air and evaporating what's left of the cloud. The result of this is that the clear air through which we get to see sunsets is usually fairly stable, even when it does not contain temperature inversions.
Because the lower atmosphere is frequently overturned by convection, it's called the troposphere. The cold, dry region above it is the stratosphere. Above about 20 km height, you can see a warm region, where the atmosphere is heated by ozone's absorption of UV sunlight; this is the infamous “ozone layer” that has been modified by man-made pollution.
These upper layers contribute little to atmospheric refraction, partly because they are much less dense than the troposphere, and partly because any line of sight from the ground crosses the upper layers at angles farther from grazing.
Notice that this profile is physically impossible, because it has sharp, angular corners. As explained on another page, heat transfer in the real atmosphere necessarily makes all changes in lapse rate smooth, not abrupt like this.
For many purposes, the smooth transition regions are too thin to worry about. Typically, they are only a few meters thick; this would not be visible at the resolution of the plot shown above. But they play an important part in producing visible features in mirages and sunsets, when — as often happens — such regions occur close to the observer. For example, the width of the mock-mirage flash depends on these transitions; and they produce enormous refraction at the edges of ducts.
But the lowest corner in the Standard Atmosphere profile occurs at 11 km, which is so far above most observers' heads that the corners shown here would have no effect in actual sunset and mirage simulations. So, in doing such calculations, I usually adopt the Standard Atmosphere profile in the upper atmosphere, and adjust just the lowest parts to produce the features I'm studying.
With the advance of aeronautics and the science of artillery, engineers and specialists in these fields have come to require a specific knowledge of the varying states of the atmosphere from the ground to very great elevations. This has led to the introduction of a conventional term commonly known as the standard atmosphere , which pretends to specify the normal or average condition. As is well known, the “standard atmosphere” is never found; that is to say, at no time or place do “standard” or average conditions of all the meteorological elements at all altitudes simultaneously occur.The constant lapse rate of 6.5° per km in the troposphere was suggested by Prof. Toussaint, on the grounds that
… what is needed is … merely a law that can be conveniently applied and which is sufficiently in concordance with the means adhered to. By this method, corrections due to temperature will be as small as possible in calculations of airplane performance, and will be easy to calculate. …
The deviation is of some slight importance only at altitudes below 1,000 meters, which altitudes are of little interest in aerial navigation. The simplicity of the formula largely compensates this inconvenience.
The above quotations are from the paper by Gregg (1920), who was then the Chief of the Aerological Section of the U.S. Weather Bureau. The early motivations for this simplified model were evidently the calculation of aircraft performance, and the construction of ballistic tables, where air resistance is important.
Unfortunately, it is precisely the unphysical and inaccurate region below 1000 m that is most important for refraction near the horizon. However, the Toussaint lapse rate, which Gregg calls “arbitrary”, is now embodied in so many altimeters that it cannot be altered: all revisions of the Standard Atmosphere have preserved it.
Furthermore, the 1976 revision of the tables changed the numerical values of tropospheric pressures from the ones published in the 1962 version, although the constants used to calculate pressures in this region were claimed to be the same in both. Comparison of these two sets of tables shows that the 1976 pressures are nearly the same as the 1962 pressures, but lack the last decimal digit. This makes the 1976 pressures systematically too low. I have not been able to learn why the pressure values were truncated instead of rounded. (This error continues into the stratosphere, up to almost 50 km.) Anyone who wants to use those tables should be careful to use the 1962 pressures, or else to recalculate accurate values.
In fact, careful examination of the 1962 Tables shows that even the pressures there were truncated instead of rounded. This error was finally corrected in the 1993 ICAO version of the Standard Atmosphere, which also made minor changes in the adopted values of mean molecular weight and universal gas constant. This changed the value of the tropospheric polytropic index from
4.2558761132784904
to
4.25587974247581744045...
A more detailed discussion of atmospheric models and their relation to calculations of refraction and extinction is in my 2022 paper in Comptes Rendus. Physique 23, No. S1, 179–212.
Some progress in this direction has been made by Marcel Tschudin: see his papers in Applied_Optics and The Observatory.
Copyright © 2002, 2004 – 2007, 2012, 2025 Andrew T. Young
or the
GF pictures page
or the or the GF home page