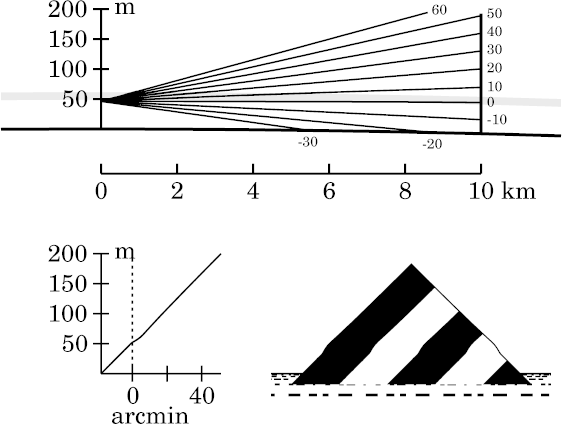
The target-distance effects are shown on this page, for a couple of different heights: one just inside the bottom of the duct, at 46 m height; and the often-used height of 54 m, near the middle of the duct.
As on the eye-height page, most of the examples here will contain a link to the corresponding un smoothed (or zigzag-profile) model simulation. Also, the discussion here concentrates on the additional effects produced by smoothing the edges of the inversion, rather than the gross effects such as towering , stooping , and image inversions like the superior mirage and Wegener's Nachspiegelung . For an explanation of these effects, see the zigzag-profile page.

Instructions for using the
[align]
links are found
here.
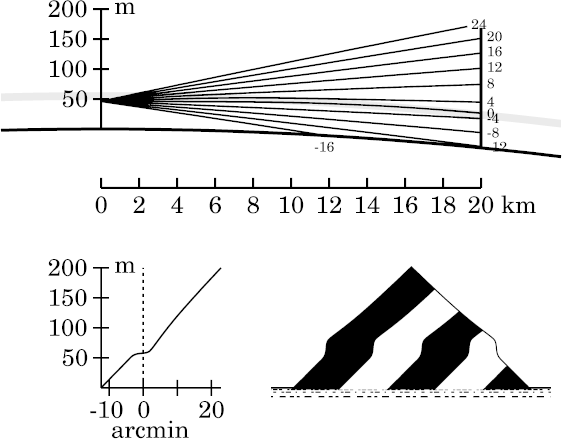
(To see the effect of varying the eye height at this distance, look
here.)
The difference is best understood by looking at the transfer curve.
Just above the astronomical horizon, at about +1′ altitude, the
zigzag model has a short vertical segment there; but here, the smoothing
of the temperature profile has made the transfer curve smooth, instead.
So, smoothing the thermal profile has eliminated that segment of the
transfer curve, and the corresponding horizontal shelf at the top of
Wegener's miraging strip.
This case is discussed further on the
page
dealing with the effects of eye height.
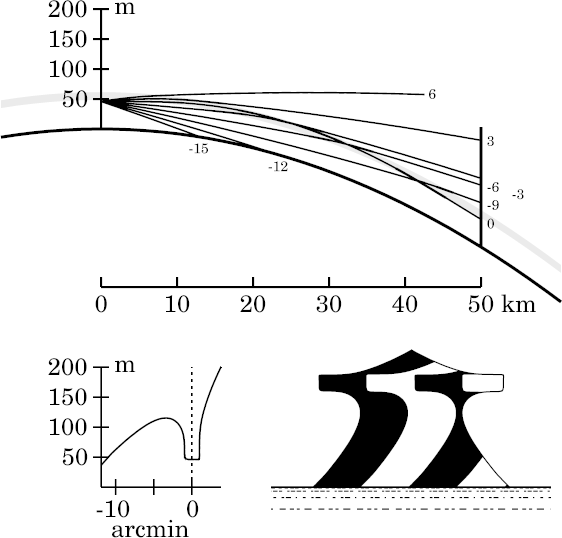
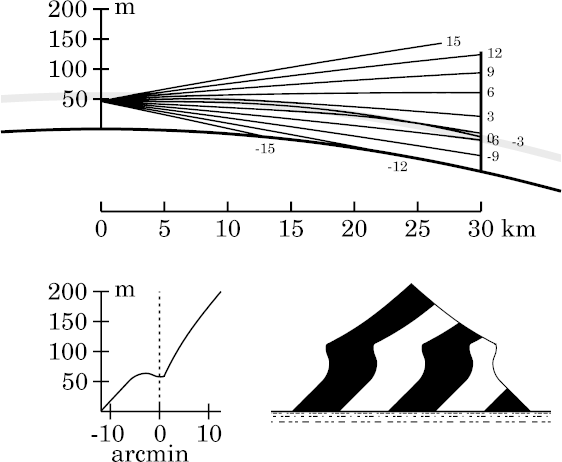
The distinctive effect of the smooth upper edge on the thermal inversion is to capture rays near the upper edge of the miraging strip, so that they approach Kummer's circulating condition, where the ray curvature matches that of the Earth.
A nearly-circulating ray at the top of the strip meets the target just at the top of the inversion. But just below this critical level, a ray remains near the top of the inversion for a considerable distance, and then bends back down, meeting the target considerably lower. A little lower still, a ducted ray eventually bends down so that it meets the target at the bottom of the duct, near 46 m. This last ray is the one at the tip of the lip in the present image; it meets the target lower than any other ducted ray. As the target is widest (within the duct) at the bottom of the duct, such rays reach the widest slice through the target.
Rays that are slightly lower at the observer don't get close enough to
the circulating level to meet the target at the bottom of the duct; so
they show the observer a higher level on the target, where it's narrower.
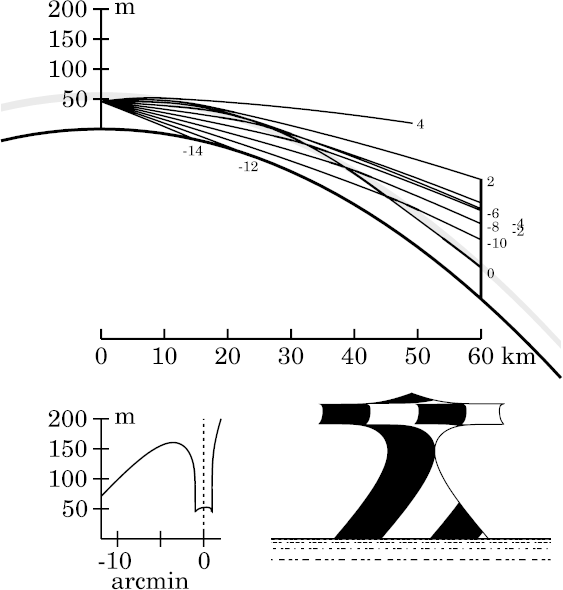
Notice that Wegener's miraging strip is completely separated from the direct view of the target, below it. At this range, we see only the tip of the target above the apparent horizon. An inverted image (Wegener's Nachspiegelung ) of its top appears just underneath the miraging strip, which is filled with an enormously stretched image of a thin slice of the target, and decorated with enormously compressed images of the 50-m level of the target (i.e., the sharp lips). Finally, the strip is surmounted by a very compressed erect image of the top of the target.
(Because of a quirk of my software, I can't produce a corresponding simulation for the zigzag model at this distance.)
It's also useful to compare these mirage simulations with
sunset
simulations
for the same model and eye height (46 m).
Of course, Wegener's miraging strip appears
blank
in the sunset images.
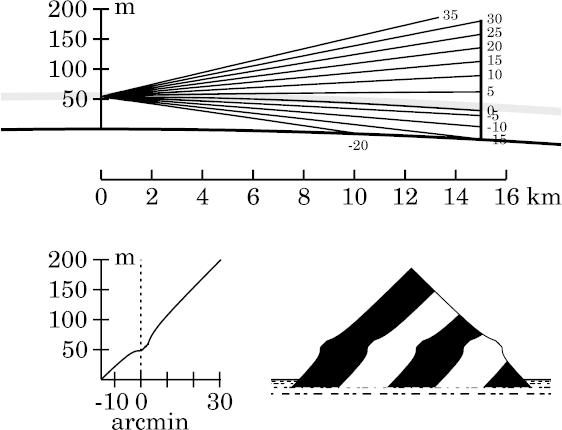
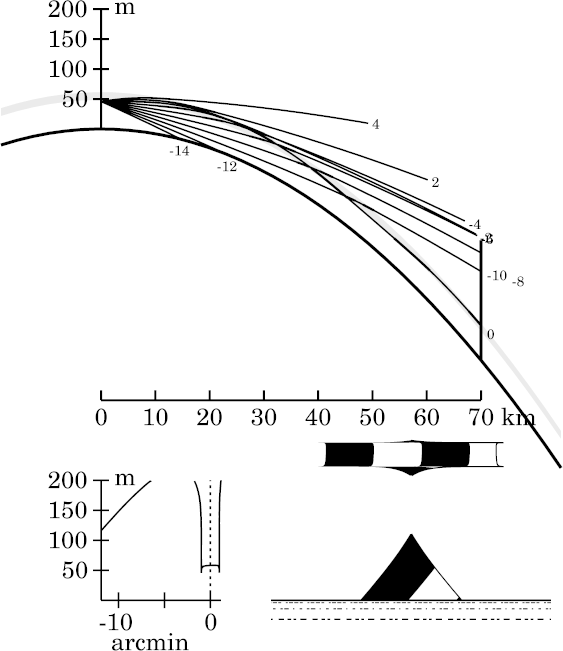
The image still resembles that for the zigzag model; but at this range, we finally see some smoothing of the image due to smoothing the inversion.
(To see the effect of varying the eye height at this distance, look
here.)
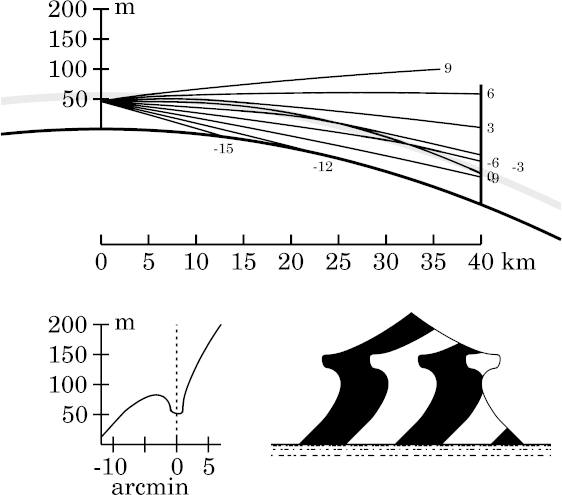
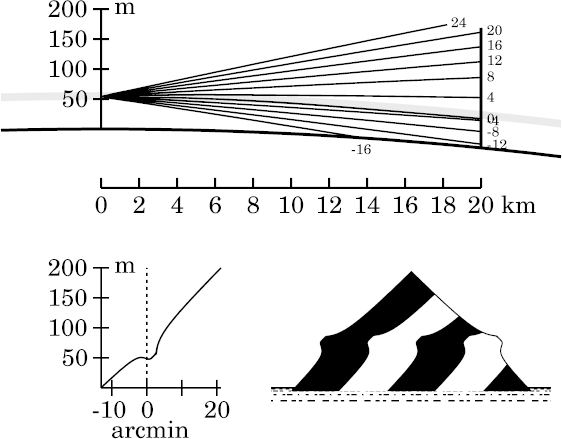
Another interesting phenomenon here is the difference between the shape of the ray at +3′ here and in the zigzag model, where it's bent down considerably more. This ray is nearly horizontal when it reaches the top of the inversion, so it spends a long time just below that height (60 m). Because of smoothing the temperature profile, the ray curvature between 59 and 60 m is appreciably weaker here than in the zigzag model. Other rays are much less affected.
This difference in the +3′ ray remains a prominent feature of the
next several simulations, at increasing ranges.
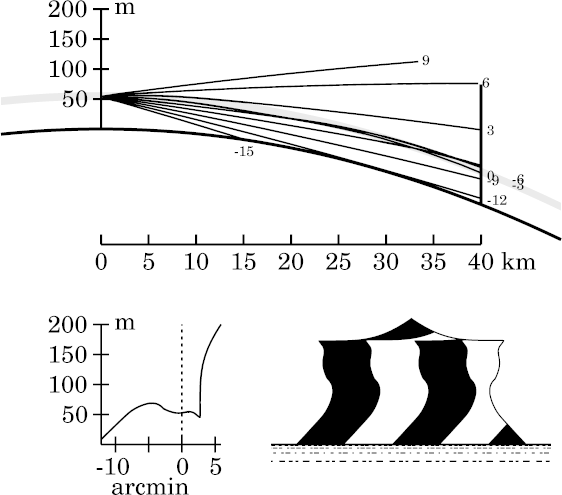
The transfer curve also shows why the +3′ ray is so strongly affected by smoothing the inversion: it strikes the target at a height near 120 m, which is in the upper part of the nearly-vertical section of the transfer curve.
(To see the effect of varying the eye height at this distance, look
here.)
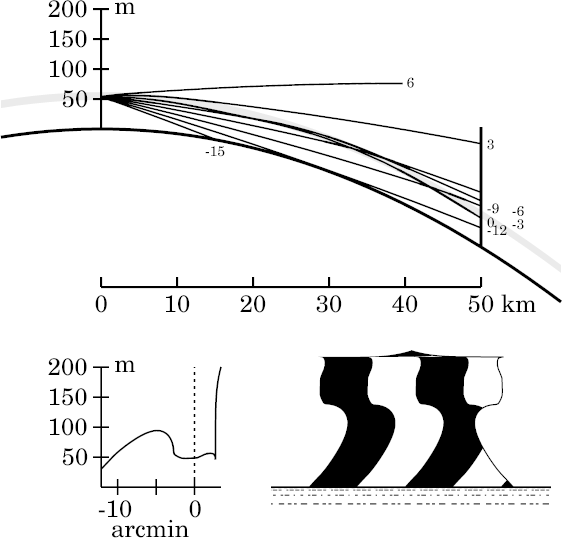
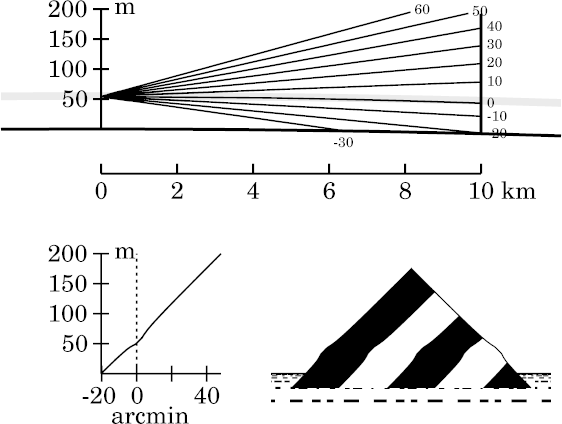
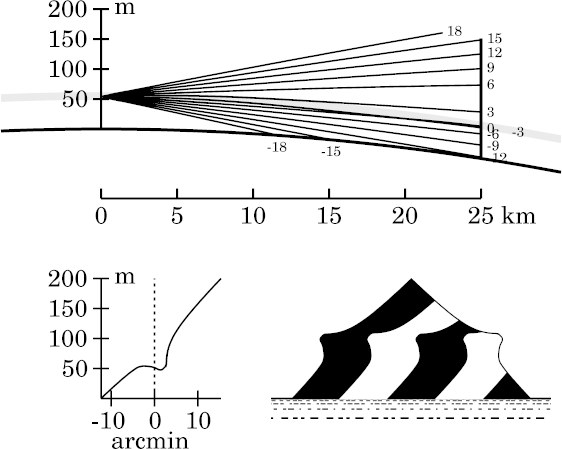
While the lip has become a spike here, other features at lower altitudes that were sharp and angular in the zigzag model have become smoother and less obvious here.
As usual, smoothing the inversion has made the miraging strip slightly
narrower. This allows more of the target to be seen just above the
strip.
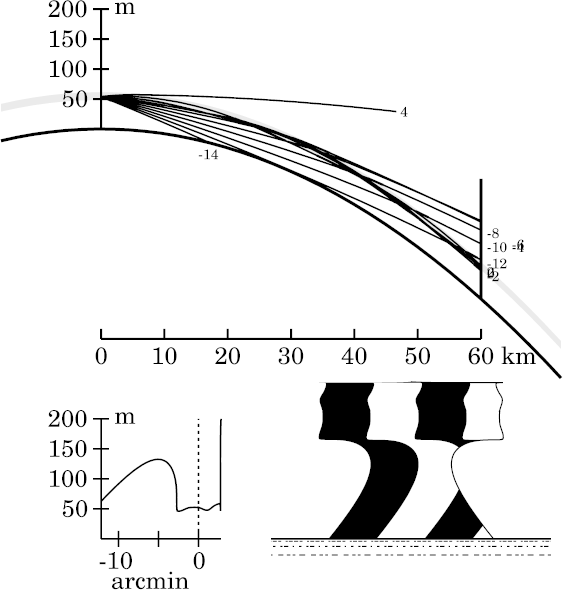
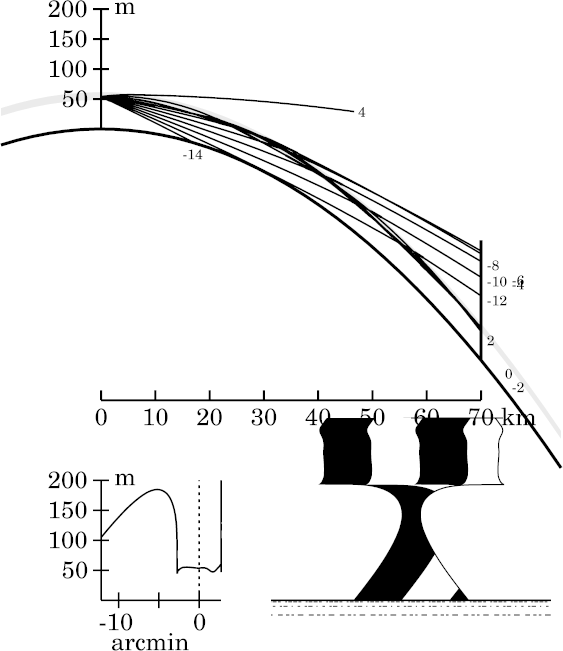
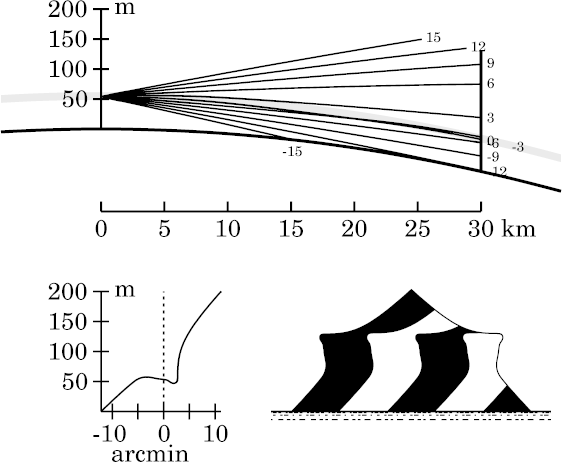
Notice the spike developing at the lower edge of the miraged strip here, and the increasing complexity of detail within the strip — especially, the extreme vertical stretching (towering) in its lower half.
Copyright © 2009 – 2012, 2020 Andrew T. Young
or the
introduction to all mirage simulations
or the
main mirage page
or the
GF home page
or the website overview page