In the 17th Century, everyone assumed that the atmosphere terminated abruptly in a smooth surface where it met “the æther,” just like the smooth surface where still water meets the “subtler” medium of air. (The æther was supposed to be subtler still than air; so, why not? The gas laws were not known.) This picture of a homogeneous layer of air surrounding the Earth goes back at least to a work on optics attributed to Ptolemy, which says that “at the surface between air and ether, there is a refraction of the visual ray according to the difference in density between these two media.”
This view had been explicitly adopted by Kepler in his failed attempt to understand refraction, and it was adopted by Giovanni Domenico Cassini as well.
Unlike Kepler, Cassini knew the sine law of refraction. And it was a simple exercise in elementary trigonometry for him to apply it to the uniform atmosphere, thus making the first quantitative model for astronomical refraction.
Cassini's model is so simple that anyone who had trigonometry in high school can follow it. Here's how it works:
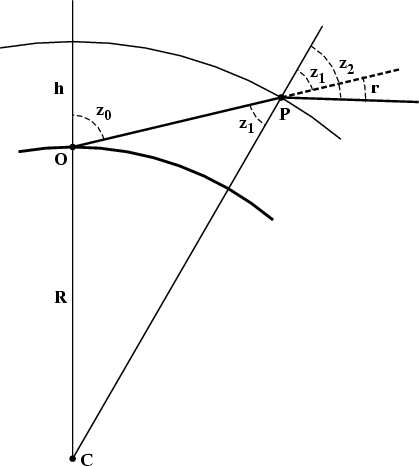In the diagram at the left, the heavy arc represents the surface of the
Earth, with radius R and center at C, and the thinner arc at a
height h above it is the surface of the (uniform) atmosphere.
The observer at O sees a star (off to the right somewhere) at
apparent zenith distance z0, in the direction of the dashed
line.
The ray OP from the star entered the atmosphere at the point P. Because the local vertical there is in the direction from C to P, which is different from the local vertical through O, the ray meets the vertical at P at an angle z1, which is less than z0.
Because of the refraction that occurs at P, the ray direction outside the atmosphere is different: the ray meets the local vertical there at an angle z2, which is bigger than z1. If the refractive index of air is n, the law of refraction tells us that
So much for the law of refraction. The nice thing is that we can calculate the sine of z1 from the sine of the observed zenith distance, z0 . If you recall the Law of Sines for plane triangles, and apply it to the triangle OPC, you'll see that
But the sine of the angle COP is the same as the sine of its supplement, z0 . So we have:
or
Now that we have sin z1 , the law of refraction gives us sin z2 :
and consequently
But (as you can see from the diagram above) the refraction, r, is just the difference of these two angles:
So, because we already had an expression for sin z1 a few lines above:
That's it! We're done. This is Cassini's refraction model.
Copyright © 2003 – 2006, 2012 Andrew T. Young
or the GF home page
or the
overview page