The picture at the right shows the relation between the Omega and the
inferior-mirage green flash: the flash occurs at the
fold line,
where the “feet” join the body of the Omega.
As there seems to be considerable interest in the Ω shape produced by inferior mirages over water, I thought it would be useful to provide more information about this phenomenon. (I already have a page devoted to George Kaplan's photos of it, which compares theoretical models with the observed shapes; see also Laurent Laveder's time-series showing the development of the Omega, and Bob Harrison's photos of an Omega sunrise.)
The picture at the right shows the relation between the Omega and the
inferior-mirage green flash: the flash occurs at the
fold line,
where the “feet” join the body of the Omega.
The explanation of the shape is very simple: the “feet” of the Ω are just inverted images of the parts of the Sun directly above them — remember that refraction only moves images vertically, not horizontally. The inverted part of the image, below the fold line, is an inferior mirage.
However, this inferior mirage over warm water is often very inconspicuous. Why is it occasionally so spectacular? The answer begins with the temperature profile that produces inferior mirages.
The temperature profile
above a heated surface has been studied by the boundary-layer
meteorologists. When you calculate refraction for that profile, you
certainly get something close to what's observed. And the
simulations
of these inferior mirages show what kinds of alterations you get by
changing the parameters of the profile.
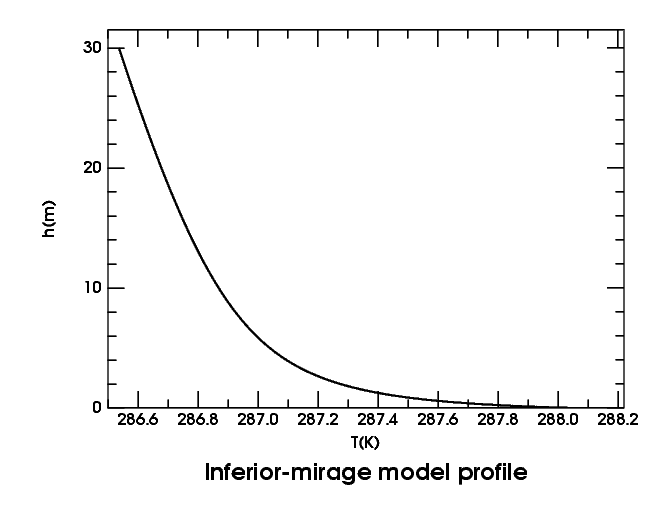
Here's the lowest 30 meters of the temperature profile I've used to make most of the inferior-mirage simulations. At the upper left, it becomes a straight line, with the adiabatic lapse rate. More important is the curved part near the sea surface: notice that the temperature increases more and more rapidly, the closer you get to that surface.
The most obvious parameter is the temperature difference between the warm water and the cool air. But just where should one measure these temperatures? There's a continuous change in temperature through several meters of air above the surface of the water (and, in fact, a similar change in the water just below the surface). So you really need to measure the change in temperature gradient with height. Fortunately, there's a parameter in the standard form for this profile that describes this.
A less-obvious parameter is the height of the waves. If the waves are high, you don't see very close to the water (except just at the wave crests). In fact, the waves cut off your view of the best part of the inferior mirage. So the lower the waves, the more of the mirage you get to see. That's a big ingredient in the showiness of the Omega right there: low waves make big feet.
Finally, there's the height of the eye. The mirage is produced by the curvature of the temperature profile in just the lowest few meters of the air. But if you're standing at the shoreline, your eye is only a little above those layers: the place where the rays are horizontal is not far from you, and the mirage subtends a large angle at your eye. If you're higher up, the horizon is farther away, so the mirage-producing layer subtends a small angle. Nearly the same part of the Sun is miraged, and nearly the same few meters of air are involved, regardless of eye height, because all the action takes place in the very lowest layers. So the inverted part of the image is squashed down into a very thin line at the horizon if the eye is high up, but makes big fat feet on the Omega if you're close to sea level.
I'll take these items in turn — starting with eye height, because that doesn't require generating variants of the model atmosphere.
Other things being equal, we expect the distance to the horizon to be proportional to the square root of the eye height. The angular height of the feet on the Omega is roughly inversely proportional to this; so fairly large changes in height are required to make a big difference in the appearance of the feet.
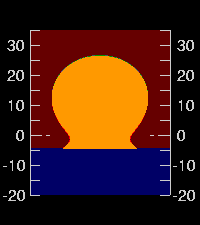
← For example, here's the Omega seen from a height of 1.5 meters. The feet are big and fat. (This is roughly what's seen by a person standing at the water's edge.)
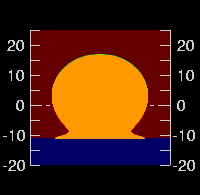
But if we move up to a height of 30 meters, we see much thinner feet. →
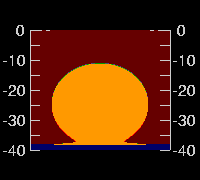
← And if we go up to 450 meters, the height from which the Vatican Observatory pictures were taken, we find the feet reduced to just a thin line at the apparent horizon.
And, sure enough, the Vatican photos show only a very thin line in their Omegas.
There is another way to think about the shrinkage of the feet as the height of the eye increases. As you can see, the angular height of the feet is larger than the narrow zone around the fold line, where the vertical magnification is large. That means that nearly all of the inferior mirage can be regarded as a reflection — indeed, it's that very property of mirages that fools the casual observer into thinking that they are pools of water (in the desert, or on hot roads).
Because this reflection effectively occurs in the lowest few meters of air — see the ray diagram for the inferior mirage, to see how strongly the rays are curved near the warm surface — it's almost as though there were a reflecting surface at (or near) sea level. Indeed, such a model reproduces the inferior mirage fairly well, except near the fold line. So let's try it for a moment.
If the Earth were flat, two rays separated by a minute of arc at the observer's eye would still differ in direction by a minute of arc after reflection by the mirage. But the Earth is curved; the ray that's higher above the apparent horizon is reflected at a more distant part of the Earth's surface, where the local vertical is tilted away from the observer. That increases the angular separation of the two rays, after reflection.
That is, we can regard the effective reflecting surface as a convex mirror, like those side-mirrors on cars that minify the reflected image. So a larger angular slice of the Sun is reflected into our minute-of-arc viewing angle: the image is reduced in height.
And the higher the eye is above the Earth's curved surface, the more of the curved surface of this mirror is visible. The most distant part of the surface, at the horizon, is the most foreshortened. So the higher the eye, the bigger is the image reduction. That's just what you see in those simulation frames above.
The increasing reduction of the angular height of the Omega's feet with increasing height of the eye means that you want to be close to the sea surface, if you want to see big feet on the Ω.
Now let's consider the temperature difference between air and water (or, more precisely, the change in the lapse rate with height in the convective surface layer). Reducing the curvature of the temperature profile reduces the thickness of the layer of air that produces the inferior mirage. By the argument made above, this makes the inferior mirage smaller: it's very much like increasing the height of the eye.
In fact, it really does increase the height of the eye above the fold line, because the reduced curvature of the temperature profile means you have to look closer to the sea surface to reach the curvature required to produce an inverted image (i.e., the inferior mirage). That puts the place where the line of sight is horizontal at the fold line farther from you, for a given eye height; and that makes the angular extent of the mirage smaller still. (It may be helpful to look at the ray diagram for the inferior mirage.)
So the very flat feet shown on my own Omega photograph (shown at the top of this page), which was taken from a height of 11 meters, must be due to a considerably smaller change in lapse rate with height than the model I've used.
Now let's consider the height of the waves, which prevent you from seeing all the way down to the mean sea surface. (I've modelled the waves as simply cutting off the view of the bottom of the atmosphere.)
The waves assumed in my usual inferior-mirage model (shown in the temperature profile above) are 30 cm high (about a foot, in U.S. units).
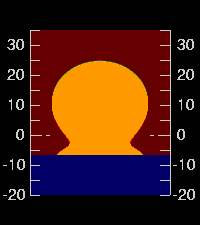
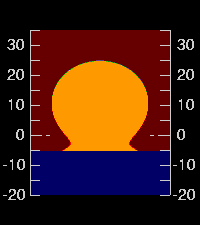
But if we adopt 10-cm waves, we get the Omega at the far left (as seen
from 4-m height); 50-cm waves give the image to its right.
With bigger waves, we see less of the feet.
If you compare these two images, paying attention to the altitude scales at the sides, you'll see that the Sun is basically the same. What's different is the position of the apparent horizon: it's a minute or two lower in the picture with the lower waves. (Because we see down into warmer air closer to the actual water surface when the waves are smaller, the apparent horizon is depressed. That can be checked with the dip diagram.)
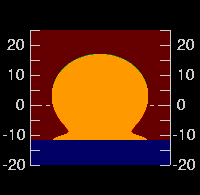
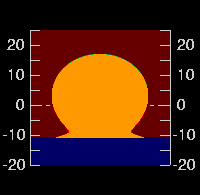
However, at a height of 30 meters, the differences are much smaller.
(As before, the frame on the left shows the effect of 10-cm waves, and the
one to its right, 50-cm waves.)
The difference can be simply accounted for by the greater distance to the
horizon — or, alternatively, by the temperature of the warmest layer
the waves let us see.
(Again, the decreasing importance of surface temperature with height
is obvious in dip diagrams.)
So: waves are important near sea level, but not very important at considerable heights.
Here are some links to photographs of Omegas, both at sunrise and at sunset. Most of them are from Japan, where this phenomenon (called the “Daruma Sun” there) has a special cultural significance, especially for Omega sunrises of the New Year. The inferior mirage is strong along the southeastern coast of Japan, because of the warm ocean current called the Kuroshio.
A collection of Omegas from the 2003 – 2004 season — this Japanese page can be translated by Google. Click on each individual image for a blowup and explanation of the details.
A similar collection for the 2004 – 2005 season, and its translation.
The Tokushima Omega Sunrise club once had an active website, with a page of pictures. (Apparently this site no longer exists; but it is available on the Wayback Machine.) Evidently, the large feet on their Omegas are due to the low waves on the waters of the bay, and the low height of the eye there. The Kuroshio current produces ideal conditions for sunrise Omegas.
Hank Hogan's sunset sequence was already cited on my green-flash pictures page, and contains an Omega.
And don't forget George Kaplan's pictures, taken from an East Coast location; the Gulf Stream probably played the same part in producing his Omega as the Japan Current does in the Japanese pictures.
More links are available here.
© 2005 – 2009, 2013 Andrew T. Young
or the GF animation introduction
or the GF home page