Folded images in mirages

Magnification and refraction

Because refraction generally raises the apparent position of objects above their geometric positions, it compresses more than a hemisphere of the real sky into the hemisphere above the astronomical horizon. So the effect of standard refraction is to compress objects seen near the horizon.

However, mirages involve rapid changes in refraction with apparent altitude. Some zones of the sky are compressed more than normal; others are compressed less, or even expanded. This effect is particularly important in the inferior mirage, for it's what makes inferior-mirage flashes thick enough to see with the naked eye. Unfortunately, the expanded zone is usually only a couple of minutes of arc wide — near the limit of resolution of the unaided eye. But even one minute of arc is about four times the normal width of the green rim, so it represents an important magnification of this feature, which is the source of the inferior-mirage flash. When seen through a magnifying mirage, the green rim can become big enough to see easily.

The transition zone

The transition between the erect and inverted images in inferior mirages is continuous: there is no sharp demarcation between the two images. At the line where the image seems to “fold over” and invert, there is great vertical magnification of the image; random landscape features appear stretched vertically, sometimes looking like the raised pile on a carpet.

This continuous transition was first noticed by William Hyde Wollaston on Aug. 22, 1800. In a paper read to the Royal Society two years later, he wrote:

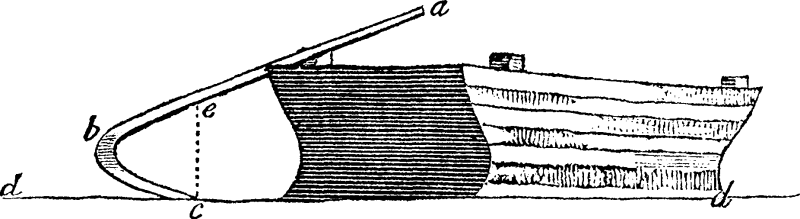
I was sitting in a boat near Chelsea, in such a position that my eye was elevated about half a yard from the surface of the water, and had a view over its surface, that probably somewhat exceeded a mile in length, when I remarked that the oars of several barges at a distance, that were then coming up with the tide, appeared bent in various degrees, according to their distance from me. The most distant appeared nearly in the form here represented; dd being my visible horizon by apparent curvature of the water; ab the oar itself in its inclined position; and bc an inverted image of the portion be. By a little attention to other boats, and to buildings on shore, I could discern that the appearance of all distant objects seen near the surface of the water was affected in a similar manner, but that scarcely any of them afforded images so perfectly distinct as the oblique line of an oar dipped in the water.

A person present at the time (as well as some others to whom I have since related the circumstance) was inclined to attribute the appearance to reflection from the surface of the water; but, by a moderate share of attention, a very evident difference may be discovered between the inversion occasioned by reflection, and that which is caused by atmospherical refraction. In cases of reflection, the angles between the object and image are sharp, the line of contact between them straight and well defined, but the lower part of the image indefinite and confused, by means of any slight undulation of the water. But, when the images are caused by refraction, the confines of the object and its inverted image are rounded and indistinct, and the lower edge of the image is terminated by a straight line at the surface of the water.

The bend at b in the image of the oar is where the vertical magnification becomes infinite, so the sloping oar appears to be vertical there. The doubly-imaged portion cbe of the oar in Wollaston's diagram corresponds exactly to the right-hand “foot” of the Omega shape produced when the Sun begins to sink below the horizon in such conditions (see the photographs of this taken by George Kaplan, as well as my simulation of such a sunset). It also corresponds to the left-hand end of the green flash produced when the green upper rim of the Sun is seen through the transition zone. In both cases, the Sun's limb is sloping from upper right to lower left, exactly like the actual oar in Wollaston's diagram.

Notice that the points marked c and e , which are connected by a vertical dashed line in the diagram, are two images of the same point on the oar. Refraction acts only in the vertical direction; so the erect and inverted images are aligned vertically. Also, note that the smooth transition from erect to inverted image is visible on the sloping sides of the barge itself.

How could Wollaston see this?

I began by pointing out that the zone of large magnification is usually too narrow to be seen by the naked eye. How, then, did Wollaston manage to notice the bend in the oar?

The answer lies in the closeness of his eye to the water. The closer the eye is to the warm surface, the larger is the angular extent of the mirage. Wollaston says his eye was “half a yard” [or half a meter, in modern units] above the surface. That's why inferior-mirage flashes are usually seen from beaches, or from the decks of ships.

Indeed, by fitting a mirror to the objective of a pocket telescope, Wollaston found that the greatest separation of the points corresponding to c and e in his diagram was seen “within an inch or two” of the surface, when the water was calm.

Why is height so important?

But why does the inferior mirage depend so strongly on height of the eye? The answer lies in the shape of the temperature profile above a warm surface.

Above a height of several meters, the temperature profile is nearly a linear function of height. The lapse rate is near the adiabatic lapse rate (about 10° C per kilometer) expected for free convection. But, as we approach the surface, the temperature increases more and more rapidly.

The increasing steepness of the temperature profile is due to the interference of the Earth's surface with the convective heat transfer: at a height h, the largest eddies (which transfer heat most effectively) cannot be larger than about h. So, as the vertical heat transfer by convection becomes less and less efficient as we approach the surface, the temperature gradient has to become steeper and steeper to maintain a (steady-state) constant heat flux.

Now, a constant lapse rate corresponds to (nearly) a constant density gradient. Optically, it's like a prism: images are displaced, but not (very) distorted. To produce distortion, we need a lapse rate that changes rapidly with height. That's exactly what the convection above a hot surface provides.

From an optical point of view, the erect image above the fold line is a virtual image: the atmosphere acts like a prism, not like a lens. (The image is displaced, but only slightly distorted.) Below the fold line, the rapid change in temperature gradient with height makes the atmosphere act like a positive, cylindrical lens, which forms a real, inverted image: the inferior mirage. This lens is located near the apparent horizon.

The power of this lens is proportional to the curvature of the density (or temperature) profile. Because of the rapid change in slope of the temperature profile, the power of the atmospheric lens varies rapidly with height. It's strong near the surface, and weak a few meters higher up. Near the surface, the focal length of the atmospheric lens is much shorter than the distance from the eye to the horizon, so the real, inverted image of a distant object is localized near the lens (i.e., near the apparent horizon). Only objects beyond the lens — beyond the horizon — can be imaged by the lens. So only objects beyond the horizon appear miraged.

But exactly at the fold line, the focal length of the atmospheric lens is exactly equal to the distance from the lens to the eye: a point on the Sun (if it's the miraged object) fills the pupil of the lens, and appears big to the eye. If that point is in the green rim, the eye sees a green flash.

So the fold line appears at the altitude where the focal length of the atmospheric lens approximately equals the distance from the eye to the apparent horizon. The lower the eye, the shorter is the distance to the horizon, and the closer and more powerful is the lens at the fold line. This makes the mirage look bigger.

For a more technical treatment of inferior mirages, in which Wollaston's bent oar is used as an example, see my 2015 paper.

A note on scale

It may help to appreciate the scale of the barge and oar in the figure above. Cargo was transported up and down the Thames estuary on these “dumb” (i.e., un-powered) barges, or lighters, until World War II. The long oars or “sweeps” were typically 20 to 30 feet long — say, 6 to 9 meters. The barges themselves were of shallow draft — about 1.5 meters — with displacements from 20 or 30 tons up to over 100 tons, and lengths on the order of 20 meters. Their beam was limited to 4 or 5 meters, because of the need to pass through locks and under bridges. The freeboard might have been 1 or 2 meters when empty, as the one in Wollaston's drawing appears to have been. The barges were steered (and propelled) with a single oar at the stem of the vessel, just as shown in his drawing.

Wollaston

Wollaston's paper contains the first occurrence of the French word mirage in the English language, so far as I know. Unfortunately, his main interest was in measuring the dip of the horizon for navigational purposes, so many later workers in atmospheric optics overlooked this paper. (The title, Observations on the Quantity of horizontal Refraction; with a Method of measuring the Dip at Sea , is not one to attract the attention of someone interested in mirages.)

Wollaston was an interesting fellow. He discovered the dark lines in the solar spectrum (later studied in detail by Fraunhofer, and so named after him rather than Wollaston) in the same year he delivered his paper on refraction (1802). In July of the same year, he discovered the metal palladium, and offered it for sale anonymously, through a dealer. Also in 1802, he measured the refractive index of Iceland spar in different directions and showed that the extraordinary ray was refracted exactly as predicted by Huygens's wave construction, which helped establish the wave theory of light. In the same year, he introduced the total-internal-reflection method of measuring refractive indices — ironically, many people still try to explain inferior mirages by total internal reflection, despite Wollaston's clear demonstration that refraction is involved.

In 1804, he announced the discovery of rhodium. A year later, he found a way to make platinum malleable, and began to sell laboratory apparatus made of platinum. He invented the camera lucida and improved the camera obscura; both played a part in the invention of photography. In 1812 he discovered “cystic oxide”, which turned out to be cysteine, the first of the amino acids to be discovered. Today he is chiefly remembered for the Wollaston prism, introduced as part of an optical micrometer he invented.

Back to the . . .
GF simulations

or the main mirage page

or the GF home page

or the website overview page