Let's first consider these distances without refraction, and then add in the complications of varying refraction. Finally, we'll consider other atmospheric effects that play a part.
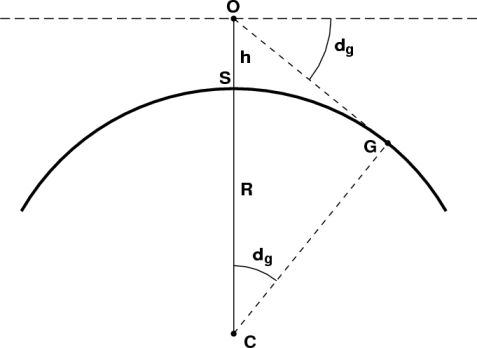
Without refraction, the matter is very simple. Here's the diagram from my dip page:
It shows a vertical plane through the center of the Earth (at C) and the observer (at O). The radius of the Earth is R, and the observer's eye is a height h above the point S on the surface. (Of course, the height of the eye, and consequently the distance to the horizon, is greatly exaggerated in this diagram.) The observer's astronomical horizon is the dashed line through O, perpendicular to the Earth's radius OC. But the observer's apparent horizon is the dashed line OG, tangent to the surface of the Earth. The point G is the geometric horizon .
Elementary geometry tells us that, because the angle between the dashed lines at G is a right angle, the distance OG from the observer (O) to the horizon (G) is related to the radius R and the observer's height h by the Pythagorean Theorem:
It's customary to use the fact that h << R at this point, so that we can neglect the second term. Then
Numerically, the radius of the Earth varies a little with latitude and direction; but a typical value is 6378 km (about 3963 miles). If h is in meters, that makes the distance to the geometric horizon 3.57 km times the square root of the height of the eye in meters (or about 1.23 miles times the square root of the eye height in feet).
Now let's allow for refraction.
Now, let's try to allow for refraction. Usually, the air is densest at the surface, so the rays of light are concave toward the surface; see the bending page for details.
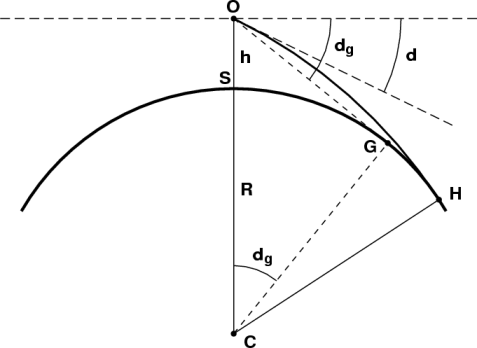
The solid arc OH now represents the curved line of sight; H is the (refracted) apparent horizon. Notice that refraction lets us see a little farther, if the ray is concave toward the Earth, as shown here.
If we can assume a constant lapse rate in the air between the eye and the Earth's surface, and if the observer's height h is small compared to the 8-km height of the homogeneous atmosphere , then we can assume the curved ray is an arc of a circle. This assumption makes things easy, because the relative curvature of the ray and the Earth's surface is all that matters. In effect, we can use the previous result, but just use an effective radius of curvature for the Earth that is bigger than the real one.
This assumption is made so often that it's conventional in surveying and geodesy to use a “refraction constant” that's just the ratio of the two curvatures. A typical value of the ratio is about 1/7; that is, the ray curves about 1/7 as much as the Earth does (or, equivalently, the radius of curvature of the ray is about 7 times that of the Earth's surface).
Using this “typical” value means we should just use the formula given above, but use a value R′ instead of R for the effective radius of the Earth, where
That would make R′ about 7440 km, so that the distance to the horizon in kilometers is about 3.86 km times the square root of the height in meters (or about 1.32 miles times the square root of the height in feet).
In fact, this latter result (for English units) is nicely summed up by the old rule that 7 times the height in feet is 4 times the square of the distance to the horizon in miles; i.e.,
NIMA has an on-line calculator that offers both English and metric units. Unfortunately, they put out far too many decimal places, giving a misleading impression of precision.
These approximations are all very handy; but how realistic are they?
Unfortunately, the refraction varies considerably from day to day, and from one place to another. It is particularly variable over water: because of the high heat capacity of water, the air is nearly always at a different temperature from that of the water, so there is a thermal boundary layer, in which the temperature gradient is far from uniform.
Worse yet, these temperature contrasts are particularly marked near shore, where the large diurnal temperature swings over the land can produce really large thermal effects over the water, if there is an offshore breeze. This is particularly bad news for anyone standing on the shore and wondering how far out to sea a ship or island might be visible.
It gets worse. While the dip of the horizon depends only on an average temperature gradient, and so can be found from just the temperatures at the sea surface and at the eye, the distance to the horizon depends on the reciprocal of the mean reciprocal of the temperature gradient. But the structure of thermal boundary layers guarantees that there will be large variations in the gradient, even in height intervals of a few meters. This means that on two different days with the same temperatures at the eye and the water surface (and, consequently, the same dip), the distance to the horizon can be very different.
To an observer within such a super-refracting inversion, the earth's surface appears to be concave instead of convex. Also, because these inversions are limited in thickness, the distance to which you can see will be limited by the highest visible ray that is trapped in the duct produced by the strong inversion. That limiting ray corresponds to a “false horizon” a few minutes of arc above the astronomical one. If the limiting ray has very nearly the Earth's curvature, you could see a long way; if the difference of the curvatures is large, the false horizon may be only a few kilometers away.
If the ray curvature exceeds the Earth's curvature everywhere below the observer, every horizontal ray in this region bends down to strike the surface at a small angle. Then no ray can be tangent to the Earth's surface, so there is really no true horizon in the usual sense — only the top of the duct, which acts as a (false) “horizon surface” that looks like an apparent horizon to all observers. Its dip is positive for observers above the duct, and negative for observers within the duct. This case was studied by Hasse (1960).
However, if the super-refracting inversion does not extend down to the surface, there are additional complications. An observer who is beneath the inversion, but still within the lower part of its duct, can see three horizon-like boundaries. The lowest is the usual sea horizon; but above it, there is a superior mirage — an inverted image — of a more distant sea horizon. And above that is Hasse's false horizon.
So the nice-looking formulae for calculating “the distance to the horizon” are really only rough approximations to the truth. You can consider them accurate to a few per cent, most of the time. But, occasionally, they will be wildly off, particularly if superior mirages are visible. Then it's common to see much farther than usual — a condition known as looming .
Still, even with those caveats, it's of interest to consider how far the eye can see under different conditions. Usually the visibility is limited by scattered light in the lower atmosphere; see
Craig F. Bohren and Alistair B. Fraserfor details. Even under extremely clear conditions, it's unusual to see more than a couple of hundred kilometers.
“At what altitude does the horizon cease to be visible?”
American Journal of Physics 54, Issue 3 (March, 1986) p. 222
However, there is one situation in which objects can be made out at great distances: when they are silhouetted against a bright background, such as the setting Sun, or (just after sunset) a bright twilit sky.
Here in San Diego, we rarely can see San Clemente Island, about 125 km offshore. The top of the island should just be visible above our horizon with normal refraction, but it's concealed by “airlight” during the day. Even in the clear air of a “Santa Ana,” which causes looming and raises more of the island above the apparent horizon, it's often hard to make out.
But just after sunset, the island is often visible, if you know where to look. The air between you and the island is only dimly illuminated after sunset, but the sky behind the island — i.e., the air beyond the horizon that is still in direct sunlight — is still fairly bright. Then the silhouette of the island is striking, even if it had been invisible a few minutes before sunset.
The Sun itself can be seen through a long duct when it is several degrees below the astronomical horizon; however, its image is then so distorted that any intervening terrestrial object (such as an island, a mountain, or even a cloud) would probably also be so distorted that its silhouette against the Sun would be unrecognizable. Some extreme claims can surely be discounted, such as Jessen's 1914 illusion. (Jessen claimed to have seen a mountain nearly 900 km away, but he certainly did not; Korzenewsky (1923), who refers to this report in a footnote, somehow inflated that to 1177 km.)
What's the record for visibility without help from the silhouetting effect? I think that might belong to the report of the expedition led by Korzenewsky (1923), who reported seeing snow-capped peaks of a mountain range 750 km away. Conditions were perfect: the lower atmosphere was in shadow at sunset; the peaks were quite high (4650 meters, or over 15,000 feet); they were covered with white snow, increasing their visibility; and there must also have been considerable looming to bring these distant features above the observers' horizon. As the observation was made on June 1, near the peak of superior-mirage season, the looming is not improbable, though the amount required is hard to believe. The observers themselves were in the deserts of Turkestan [now southeastern Kazakhstan] at a height of nearly a kilometer, where the dryness of the air favored extreme clarity, and looking across a broad, sandy depression. And, of course, much of the air path was in thinner air well above ground level, because of the mountains' height.
For less extreme, but very reliable, observations, consider some listed by Commander C. L. Garner of the Coast and Geodetic Survey in 1933. He says that instrumental measurements were made in both directions “between Mt. Shasta and Mt. St. Helena in California, a distance of 192 miles.” [That's 309 km.] Apparently this was done in normal conditions, with no looming ; heliotropes having 12-inch [30-cm] mirrors were used. He also credits the 1911 sighting of the Fairweather Mountains in Alaska from the ship Explorer in the Gulf of Alaska, 330 miles [531 km] away.
Without resorting to an artificial light source, there's the example of mountains in Corsica, seen repeatedly from Genoa, Italy, at a distance of over 260 km. The best visibility was just before sunrise and just after sunset, when the distant peaks were silhouetted against the bright twilit sky: the lower atmosphere was in the Earth's shadow, while the upper troposphere was still lit by direct sunlight. These observations were extensively discussed by Maraldi four centuries ago.
A thorough modern discussion of these matters is given by
Michael Vollmerwhich brings the subject up to date. That paper has many good references. Recently, its author has pointed out a Polish website at https://dalekiehoryzonty.pl that has lots of photographs showing features on the horizon more than 200 km from the camera.
“Below the horizon — the physics of extreme visual ranges”
Applied Optics 59, No. 21, pp. F11-F19 (20 July 2020)
If you'd like to explore the consequences of various (constant) values for the lapse rate, I have a JavaScript calculator here. It uses the simplistic circular-ray approximation, so take its calculations with a grain of salt. In any case, it's too simple-minded to handle the complications produced by ducts, so beware of trying to run it with strong thermal inversions.
Copyright © 2003 – 2008, 2010, 2012, 2016, 2020 – 2023 Andrew T. Young
Didn't find what you were looking for? Try the glossary or the alphabetical index.
or the
mirage page
or the alphabetic index
or the Overview page