When the Sun is low, but still a couple of degrees above the horizon — say, about ten minutes before sunset — dispersion is large enough to make the green upper and red lower limbs visible, if the telescopic image is projected on a sheet of paper. Here's a simulation of the appearance (for the Standard Atmosphere) when the upper limb is 2° above the astronomical horizon:
You can see that the upper limb has a narrow green rim, and the lower limb
has a red one. The rims aren't very conspicuous here; but in fact this is a
realistic simulation of the rims at about their most prominent. The fact
is, they're not very wide at all, even under the best conditions.
You might think that the rims would be more obvious closer to the horizon. But it turns out that there's a trade-off between increasing refraction (and hence, width of the rims) and increasing extinction. (Remember that refraction and extinction are nearly proportional, near the horizon, because of Laplace's theorem.) As the Sun approaches the horizon, the increased atmospheric reddening rapidly overwhelms the green rim, making it fainter and fainter. And the red rim also becomes less prominent near the horizon, because the whole disk of the Sun becomes redder, so there's less color contrast between the disk and the lower red rim.
As a result, the colored rims are most prominent at altitudes between 1 and 2 degrees. You can compare the simulation with some nice photographs of the colored rims taken by Laurent Laveder (be sure to click on the small images to see larger versions; and don't miss the second page of pictures.) These fine examples were taken just in this optimal range of altitude, and in very clear conditions.
In fact, the simulation here assumes extremely clear conditions. The aerosol optical depth at 550 nm wavelength above the observer (located 10 meters above sea level) is only 0.02 — an improbably small value. Typical conditions would have an aerosol optical depth of 0.1 or so. Even under very clear conditions, the aerosol optical depth near sea level is hardly ever less than 0.05.
But even these small aerosol opacities in the vertical direction correspond to quite considerable optical depths at the horizon. If the aerosol were uniformly mixed in the atmosphere, the horizontal optical depth would be about 40 times the vertical one. But in reality, the aerosol in concentrated in the boundary layer; I've assumed an aerosol scale height of 1 km in these simulations, which makes the horizontal optical depth just over 100 times the vertical value.
That means that the optical depth in the green, at 550 nm wavelength, is usually about 10. But the aerosol optical depth is almost inversely proportional to wavelength, so the optical depth in the red-orange at 610 nm is only about 0.9 as big: about 9. This means that the green rim is attenuated by about a factor of e = 2.718 … , relative to the red disk, at the horizon.
The aerosol opacity falls to half of its value at the horizon at an altitude of only 42 minutes of arc, if we assume a scale height of 1 km. That means that more than half of the excess attenuation of the green light occurs in a space only one and a half solar diameters wide at the horizon. The great majority of the reddening is in the last degree at the horizon.
Now let's examine the green rim more closely. Here are some enlarged simulations, at intervals of a degree, from the astronomical horizon up to 5° above it. Once again, the Sun is seen through the Standard Atmosphere from a height of 10 meters.
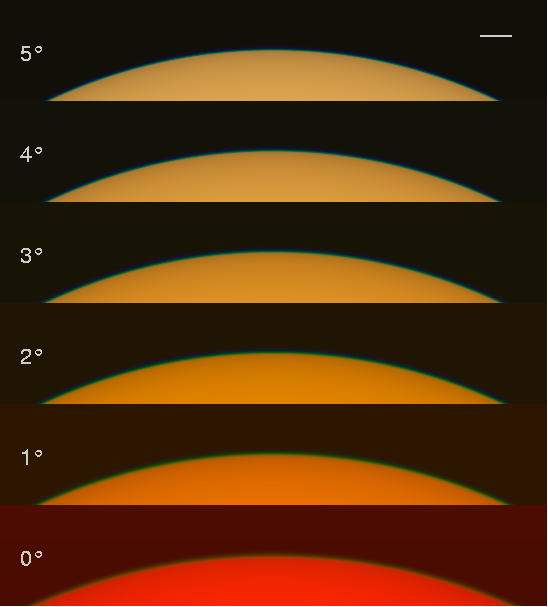This image shows the variation in appearance of the green rim with
apparent altitude. The sub-panels are marked at the left side
with the altitude at the
top of the disk. The scale bar in the upper right corner is one minute
of arc long, and about 1/16 of a minute (3.75 seconds of arc) in thickness.
(A minute of arc is about the limiting resolution of the human eye.)
Each sub-panel has been made as bright as possible, without saturating the image; this is similar to the adjustment of exposure a photographer has to make in following the Sun as it sets. If the brightnesses were not adjusted, the bottom panels would be too dark to see well.
Here, a slightly more realistic zenith optical depth of 0.03 has been assumed for the aerosol. Even so, this represents extremely clear conditions. The optical depth at the horizon is about 3.2, at 550 nm.
Notice how narrow the green rim becomes at altitudes above 2°. At the greatest altitude shown here (5 °), a little blue is detectable in the green rim; but the rim is so narrow that this is difficult to see, even at the scale shown here. (What you see on your screen is magnified about 20 or 30 times, compared to a naked-eye view of the low Sun.)
For a real-world comparison, see Laurent Laveder's pages showing how the blue gradually fades away as the Sun approaches the horizon. In his photographs, the blue is occasionally emphasized by irregular atmospheric structure — probably waves on the inversion that caps the convective layer. (His sunset has an Omega shape, so it ends with an inferior-mirage flash, rather than the undistorted rim shown here.)
Even at its widest, the apparent width of the green rim isn't much greater than the thickness of the scale bar. That's because the increasing extinction at short wavelengths never allows the whole green part of the spectrum to appear, at the lower altitudes where the rim is widest.
The faintness of the rim at the astronomical horizon (bottom section of the figure) shows why an isolated green rim — the “textbook” flash — isn't a plausible explanation for most real green flashes. As Dietze found, it's only a little brighter than the horizon sky, and not prominent enough to be apparent to the naked eye. If a more typical optical depth were assumed, the green rim would be completely invisible at the horizon.
However, there is one place where green-rim flashes can be seen, even with the naked eye. The rapid decrease in extinction and atmospheric reddening with altitude means that if the rim is occulted by an elevated obstacle (such as a mountain, or even the ridge line of a building), so that the upper limb is isolated at an apparent altitude of a degree or two, where it is most visible, there's a chance of seeing this “textbook” flash with the naked eye.
Furthermore, because the decrease in extinction with altitude is even more pronounced at shorter wavelengths, there's a good chance that this elevated-horizon flash will appear blue, or even violet. And, sure enough, there are numerous reports of blue and green flashes seen over mountains: Maggi's 1852 observation that “when the Sun sets behind distant mountains, the last disappearing edge is dyed a vivid blue”; de Maubeuge's 1886 report of a green flash over mountains 1 to 2 degrees above the horizon — an observation repeated over the Sinai in 1898; Lord Kelvin's 1899 blue sunrise over Mont Blanc; B. G. Escher's 1929 blue flash and green ray seen over the Sinai; multiple green flashes seen at high latitudes as the midnight Sun passed between distant peaks — a 1983 report of multiple blue flashes by Baxter nearly echoing a very early green observation by Henry Bedford in 1879; etc. This mechanism may also explain some cloud-top flashes.
Copyright © 2005 – 2008, 2013 Andrew T. Young
or the GF pictures page
or the GF home page
or the alphabetic index
or the website overview page