Sometimes I need to reproduce plates or figures from 19th-Century works. You'd think this would be simple enough: just scan the figure, threshold the image to make the inked areas come out black and leave the paper white, and convert the bi-level (monochrome) image to PostScript form for publication.
Here's an example. The image at the right was scanned when I wanted to
reproduce the shadings used to depict spectra by means of a wood-engraving
in H. Kayser's Handbuch der Spectroscopie ; I've
reduced the resolution
by a factor of 8 here to make the image fit on the screen.
(This grayscale version looks much like the original printed page.)
If we look at the histogram of the original (not the reduced!) image, we
get what's shown below at the left. It's not what you'd expect: the
peaks for the black and white pixels are not cleanly separated, but
overlap considerably.
Furthermore, the white pixels seem to fall into two groups, so that the
whole histogram has 3 peaks instead of the expected 2.
(This will be explained later.)
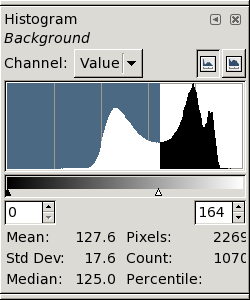However, there is a fairly well-defined minimum at
about data value 164; so let's threshold the image at that level and see
what we get. (The resulting image follows the next few paragraphs.)
Again, I've reduced the resolution of the thresholded image (which contained only black and white pixels) by a factor of 8; so what's shown here is a grayscale image. However, it shows the characteristics of the thresholded full-resolution image fairly well.
The result looks very different from the input image. The contrast has been greatly increased: what were dark grays have become nearly black. In both the lightest and the darkest areas, the details of the shading have been lost.
(This reduced image also shows some artifacts. The diffuse, nearly
vertical banding that's particularly obvious in the right half of the
image is due to aliasing of the shading lines at the reduced resolution
shown here; you can ignore that.)
So reproducing a black-and-white print isn't as simple as scanning and
thresholding. To begin with, scanners don't capture an image
perfectly: because of scattered light and optical imperfections in the
imaging, there's a certain amount of
blurring that washes out the finer
details. While this blurring isn't important for some work, it loses
appreciable detail in copperplate engravings, and even in wood engravings.
As a result, the fine lines used for shading tend to wash out. In lightly-shaded regions, the shading becomes paler; in heavily-shaded ones, small ink-free areas darken. So the light areas become lighter, and dark ones darken: paradoxically, the blurring increases the apparent contrast of the shaded areas. In fact, the histogram of such a scanned image often doesn't have a deep, clean minimum separating “ink” from “paper” pixels. (It may not even be bimodal.)
This problem is apparent in many published books that attempt to reproduce engravings. For example, the original frontispiece to Galileo's “Dialogue Concerning the Two Chief World Systems” (in Stillman Drake's translation published by the University of California Press in 1962), which appears after the Translator's Preface, is very poorly reproduced because of these effects: details are lost in both the highlights and the shadows of the scene. (Though this was produced photographically in the days before scanners and laser printers, the same problems occur in photographic imaging.)
Further trouble appears on the output side, if a laser or inkjet printer is used. The darker areas tend to block up and become solid black, increasing the contrast still more. Again, it's a problem with fine detail: even though good laser printers these days have 1200 or more dpi, they won't cleanly reproduce the delicate features in engraved shading.
Part of the problem is that scanning and image processing involve gray-scale or analog images, not binary black and white. The scattering of light within the paper makes any printed page inherently a grayscale image, even with perfect scanning and printing. So you need to think in terms of shades of gray, even though you start with black ink on (presumably white) paper, and end up with black ink or toner on white paper again. And the gray scale introduces issues of gamma and contrast and other considerations that weren't present in the original printing plate, and aren't present in the desired result.
Another part of the problem involves the incommensurate resolutions of scanners and printers. Scanners tend to have resolutions like 800 or 1600 dpi, while laser printers are typically 300, 600, or 1200 dpi. So we need to worry about aliasing and resolution problems as well.
These pages explain the various parts of the problem, and describe ways of dealing with them on a Debian Linux system.
First of all, there's a problem that occurs on both the input (scanner) and output (printer) sides: ink on paper isn't just black on white. Paper isn't a uniform white surface, and ink isn't uniformly black. Under a high-resolution microscope, you see that the paper becomes darker close to a large inked area. And the thinnest lines in engravings aren't solid black lines, but fade away gradually into shades of gray or brown.
The reason for this is that the interaction of light with paper and ink isn't all or nothing. The fibers of the paper scatter and redistribute the incident light; when there's a heavily-inked area nearby, some of the light that would have bounced around inside the paper and eventually emerged gets absorbed by the neighboring ink instead. So the apparent reflectance of the paper diminishes toward the edge of a dense black mark. (This internal scattering of light within the paper is a problem in radiative transfer. It's really a three-dimensional process; there is a one-dimensional simplification, known as Kubelka-Munk theory, but it's not fully adequate to describe the process.)
The light penetrates a surprising distance into the paper; that's why things printed on the back of a sheet “show through” on the front side. Let's suppose the light spreads laterally within the paper by a distance comparable to the thickness of the page. A typical ream (500 sheets) of paper is about 5 cm (2 inches) thick, so a sheet is about a hundredth of a centimeter, or a 250th of an inch, thick. So we'll certainly see this effect in a scan made at 600 or 1200 dpi, or more. (And the problem occurs again when the image is printed on a laser printer.)
Likewise, the fine lines of good engravings are so thin that they don't contain enough ink to be “optically thick”. If you look at them under a microscope (or at least a high-power magnifier), you'll see the finest lines are shades of gray or brown, not pure black. In very thin layers, even black ink isn't completely opaque. So, again, we have to deal with shades of gray.
Of course, when a scanned image is printed on paper, the light gets to scatter around again within the paper of the reproduced copy, so we have another round of image blurring due to radiative transfer. That means that we have to make some allowance for this in printing the scanned image.
Things are different when we view the scanned image on a computer screen — an intermediate step we have to make when we process the image. Again there's scattering of light in the screen; but this time things are a little different, because we're writing white marks on a dark background, instead of the other way around. We can minimize the screen problems by viewing the image at high magnification.
If we knew the MTF of a scanner [or, equivalently, its point-spread function (PSF)], we'd at least have the information needed to correct the scanned image for blurring by the scanner. But such information isn't usually available for scanners; their makers don't even offer typical values. In any case, we should expect that the actual blurring of a particular scan depends on defocus and other peculiarities of our particular scanner, and the properties of the ink and paper used in the original page we're trying to copy. So even a “typical” PSF or MTF wouldn't be exactly what we need.
That means we have to figure out the blurring of the image from its
internal structure. Fortunately, we know that the original page was
printed so that solid-black areas should be uniformly dark; so we can use
the edges of such areas — if some exist in the original image —
to determine the blurring, and reconstruct an approximation of the
original printing plate.
Even if there isn't a solid black area available, it may still be possible
to infer the blurring by looking at the cross-section of lines of
different widths in the image.
Here's an example. The figure at the right shows the original raw image
at low resolution. On the left below, the grayscale image shows a small
area of the second spectrum (marked “2” at the left side of
the full image),
showing the details of the complex region below the letter G
at the top edge of the full image. Notice how alternating black lines and
white spaces of different widths are used to produce shading.
Immediately below the image is a plot of the data values along its middle
row. You can see the problem: the black lines around columns
3680–3740 are actually about the same shade of gray (near 150)
as the white lines between the heavy black ones around col. 3650.
(The same problem appears again in the thin white lines near
cols. 3830 and 3930.)
So there's no threshold that cleanly separates white and black.
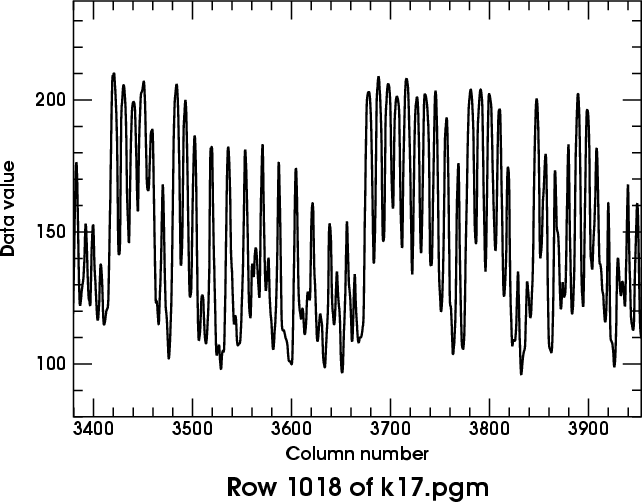
Furthermore, the black and white bars have rounded intensity profiles, instead of being approximately square on the tops and bottoms, as we should expect. This is another effect of the blurring in the scanner data.
I discuss blurring at considerable length on another page. The parameter adopted there is the period of a sinusoidal component of the image that's attenuated by a factor of 2 — not an easy value to extract from real images.
However, there are places where black and white shading bars of about equal width occur. They usually have periods of about 15 pixels (in our example image); and these features aren't seriously degraded. That certainly sets an upper limit to the blur scale.
On the other hand, there are isolated narrow features, typically about 3 pixels wide, that are clearly smeared out quite appreciably (e.g., the narrow white spaces between the broad black shading bars around column 3600 in the rowtrace shown here, and the narrow black lines around col. 3700). From these, I'd guess that the blurring length is 5 or 6 pixels.
The formula I used for restoring images uses the square of this length R; so I'll try R2 = 30. The value of the “sharpness” parameter to be used in the Gimp's Sharpen filter is then about 41; this filter is to be applied twice to obtain a reasonably well-corrected image. (See the discussion on the blurring page for the details of these calculations.)
To bracket the proper correction, I tried using sharpenings of 35 and 48
as well. The best result seemed to lie near 48; so I then tried
56 as well, to make sure I had gone far enough.
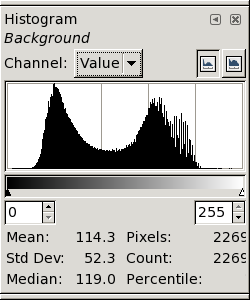Here are the resulting histograms of the enhanced images, at full resolution.
The de-blurring was done after converting the original image
to intensity, to avoid the noise-rectification problem described on the
blurring page. The conversion to
intensities made all the images darker, as explained on the
gamma
page; so these histograms aren't directly comparable to the
original
one shown near the top of this page.
← The first (at the left) was sharpened by 35 twice. It still has the double peak near the white level; clearly, this image is under-corrected.
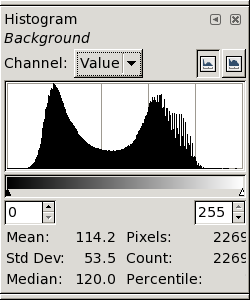
The second version (at the right) was sharpened by 41 twice. The near-white peaks are now coalescing; clearly, this version is better. →
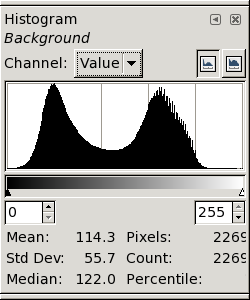← The third version, sharpened with 48, is on the left.
This seems a fairly good result; the white peak is becoming
compact. However, the histogram is starting to develop little
“feet” at its extremities, suggesting that we're starting to
amplify the noise excessively.
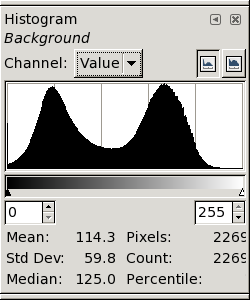Finally, on the right, we have the result of sharpening with 56.
The “feet” are now quite obvious, and the image itself shows
definite “ringing” at the black/white transitions. This is
clearly too much sharpening. →
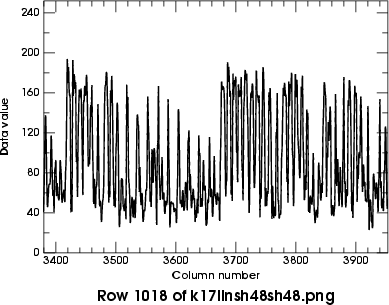
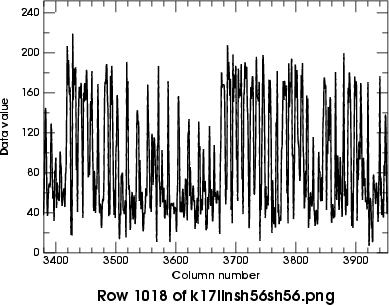
Below are the row plots for the two best versions (sharpenings of 48 and
56, each done twice) in the same region that was shown in detail
above.
You can see that the thin black and white lines that had similar
data values in the original image now have been enhanced enough that
thresholding near a data value of 100 will make them visible.
From here on, I'll adopt the version sharpened by 48 twice.
← Here is a
(reduced)
version of the sharpened image, thresholded at 100.
Thresholding has produced an image that's black where there was ink on the
original page, and white where there was just paper.
This version looks better than the one that was just thresholded without sharpening; detail has been preserved in both the lightest and darkest areas, and the overall contrast is now lower (i.e., more like the original grayscale image).
(In choosing the final thresholding level, you should allow for the subsequent lightening that must be made to compensate for the imperfect blackness of the ink on the original printed page. Therefore, pay a little more attention to preserving detail in the finest lines, and in the lightest shading rather than the darkest, if a choice has to be made.)
However, the contrast is still much higher than the original — especially in the darker areas. That's because (as explained here) the inked areas on the original page weren't perfectly black, while thresholding produces completely black blacks.
The cure for this problem (as explained here) is to add a little something to the black areas. Experimentation shows that “something” should be about 50, for this particular image.
So here's the result of incrementing the black pixels by 50.
You can see that it's a lot closer to the
original
grayscale image.
Basically, we've reproduced the original as a bi-level image (white and dark gray, not white and black). Notice that we have adjusted the color of the background from light gray (in the original scan) to white; this, together with the sharpening, gives this processed version a much cleaner look than the original.
Now we're ready to print this out.
There are several standard ways of representing shades of gray in two-level (black and white) printing. They all come under the heading of halftoning.
Although there is a well-developed theory for digital halftoning, it suffers from the same kind of weakness as Cassini's refraction theory: it's an exact solution to an idealized problem that omits essential details of the real-world problem we actually want to solve. In halftoning, the missing details have to do with the overlapping circular dots that the printer actually places on the paper, where the computer model has square pixels. The dots have to be big enough to fill in solid-black areas completely; this makes them cover more of a gray area than they should, making all the shades of gray too dark (usually, much too dark.)
In principle, we should really measure the reflectance our printer produces for each of the 256 possible gray levels, and correct every grayscale image with the inverse of that function. That's a lot of work!
Fortunately, we don't have to do all that. We carefully reduced our original image above to a bi-level (gray and white) one. So there's only one shade of gray to be rendered by the printer.
If you download my 255-shades-of-gray image, and convert it with the same halftoning method you use for printing, all you have to do is print its halftoned version, and see what input gray value makes your printer produce the desired shade of gray on paper. Then, just add that value to the black-and-white (thresholded) version. Usually, the amount you add will be more than what's needed to make a correct version on the monitor screen; I added 50 above to get the right version on the screen, but I need to add about 140 to get a version that prints properly on an HP 2420 (1200-dpi) laser printer.
You might need to adjust the value to be added until you get what you want. But basically, this should do the trick. Just remember: the gray-level adjustment depends on the printer you use, the paper you print on, what toner or ink cartridge you use, etc.; so every combination requires its own offset.
Copyright © 2006 – 2009, 2012 Andrew T. Young
or the
GF home page
or the website overview page