Symmetry in Atmospheric Refraction

Introduction

Some of the complexity of refraction phenomena can be reduced by considerations of symmetry. This page discusses several of these.

Reversibility of rays

Perhaps the simplest symmetry is fundamental to geometrical optics: the reversibility of rays. I consider reversibility in general elsewhere; but there is a particular case in atmospheric refraction that deserves special attention.

Reversibility connects the paths taken by pairs of rays at equal altitudes above and below the astronomical horizon. 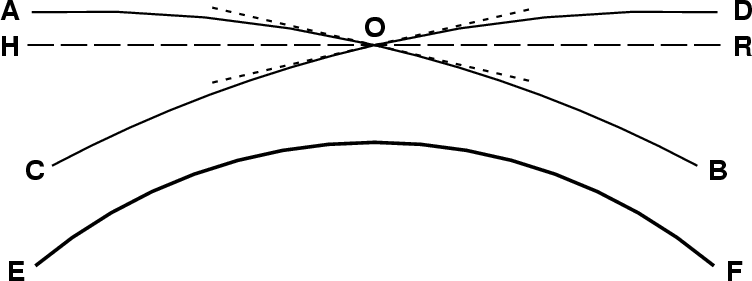In this diagram, where EF represents the surface of the Earth, the rays reaching the observer at O from B and D are such a pair; note that their tangents at O (i.e., the directions from which they appear to come) make equal angles with the local horizontal, HOR. These paths have the same shape; at each height, they have equal slopes. Essentially, they are the same shape, simply transposed (or reflected about their lowest point) so as to place the observer on either the rising or the falling half of the curve — as their extensions on the left side of the diagram show.

Symmetry of refracted rays

This immediately brings up the symmetry of the ray path itself. All refracted rays in a horizontally-layered atmosphere are symmetrical about their lowest point. (Note that “horizontally-layered” means that the refractive index is a function only of the distance r from the center of curvature of the atmosphere.)

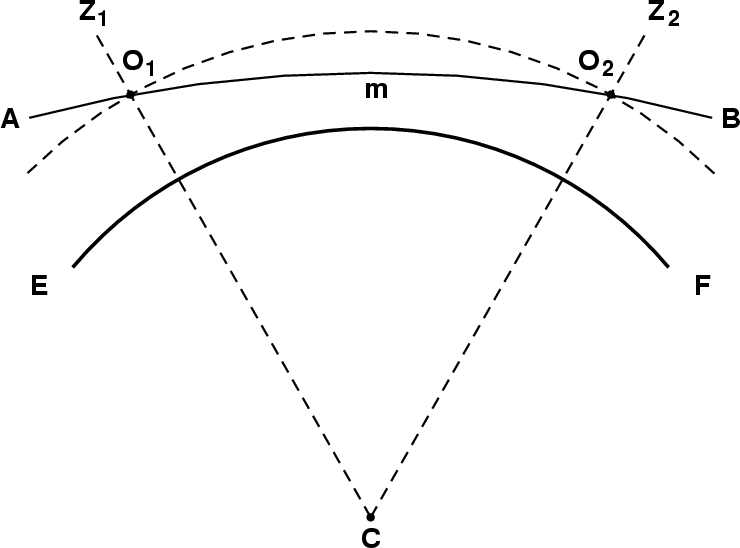As the ray AB is horizontal at its lowest point, m, the zenith distance there is 90°, which makes the sin z factor in the refractive invariant n r sin z equal to unity. (z is the local zenith distance at any point along the refracted ray.) Then the invariant is simply the value of n r at the minimum.

Note that the even symmetry of the sine function about 90° makes sin (90 + x) = sin (90 − x). Consequently, the invariant says that the curve has equal but opposite slopes on either side of the minimum, at the same value of r.

This aspect of symmetry can be used to derive the magnification theorem.

Coefficients in the series expansion

One of the most historically important devices in the theory of refraction is the expansion of refraction in powers of (tan Z), where Z is the zenith distance of the ray at the observer. One reason why this expansion is so useful is that it involves only odd powers of (tan Z); the rapid decrease in the coefficients of the terms make all the high-order terms negligible out to considerable zenith distances. So, for many purposes, the flat-Earth approximation involving only the first term is good enough out to 60° or so; and beyond that, Oriani's theorem shows that the refraction out to 75 or 80° — which is to say, the whole of the sky over which image quality is good enough to allow accurate positional measurements — is well represented by just the first two terms, which involve only the temperature and pressure at the observer, and not the detailed atmospheric structure. (On the other hand, this same argument shows that Cassini's model, which is even more accurate, is perfectly valid in this same region.)

But why are the coefficients of the even powers all exactly zero? This is not immediately obvious; and indeed, Bradley discovered empirically that the coefficient of tan²Z was negligible, and then simply assumed it was zero without proof. And even Ivory goes to the trouble of proving it by tediously evaluating the integrals involved in the coefficients. But we can easily prove it without evaluating any integrals.

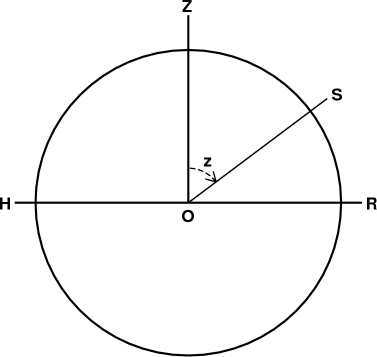
The diagram at the right shows a complete vertical circle. The observer is at O, with zenith at Z, and HOR is the observer's horizon. S is a star, whose zenith distance is z, measured positive from Z toward R. But then zenith distances should be negative when measured from Z toward H; objects in the left half of the diagram must have negative zenith distances — and likewise, negative refractions. (Perhaps the inconvenience of such negative angles explains why they are not normally used.)

Astronomers are so accustomed to considering zenith distances as positive that the continuity and smoothness of the refraction through the zenith are usually overlooked. But if we consider the whole vertical circle, regarding Z as positive on one side of the zenith and negative on the other, it's obvious that the refraction is an odd function of Z. As (tan Z) is also an odd function of Z, the only way the refraction can be expanded in powers of (tan Z) is for only odd powers to appear; the even powers of (tan Z) would be even functions, but the even part of the refraction must vanish. So the coefficients of the even powers of the tangent must also vanish.

Copyright © 2002 – 2003, 2005, 2006, 2010, 2012 Andrew T. Young

or the GF pictures page

or the GF home page