Ordinary Mock-Mirage Simulations

Introduction

Here are the ordinary mock-mirage simulations of my usual target.

Ordinary mock mirages

The same model atmosphere, with an inversion of 0.8° between 30 and 50 m, has been used for sunset simulations. I'll put the eye at a height of 55 m, just 5 meters above the top of the inversion. (The sunset simulation for 60 m eye height in this model is shown here.)

As usual, I'll start with the target a few kilometers away, to show that there's no perceptible distortion at short ranges.

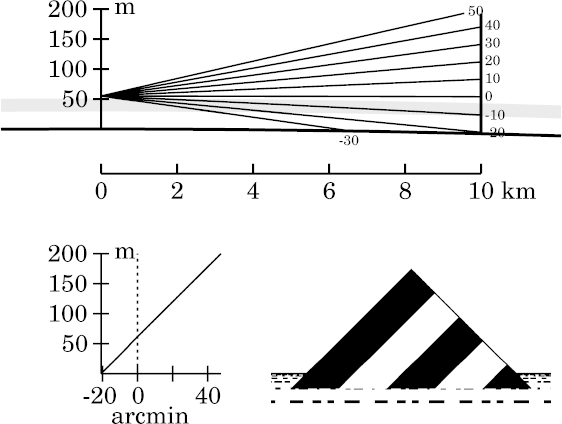
ordinary mock-mirage simulation at 10 km

Nearby target: no distortion

So here's the target at 10 km, as seen from a height of 55 m. Even at this range, the rays appear nearly straight, because the inversion (which is shown shaded in these diagrams) is so weak. The transfer curve appears nearly straight; there's negligible image distortion.

You can see that the target is much closer than the apparent “sea horizon”, both in the simulation at the right, and in the ray diagram above it. As usual, each ray is marked at its right-hand end with its altitude (in minutes of arc) at the observer.

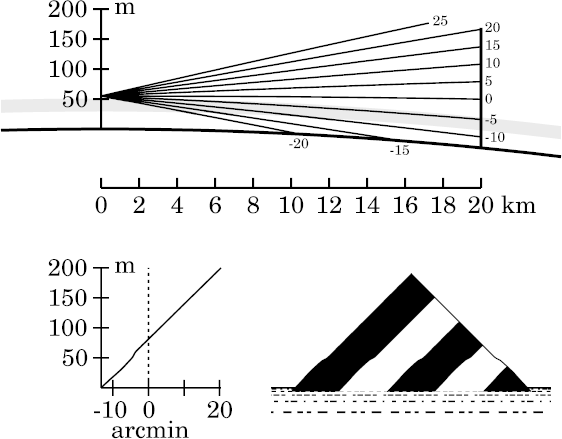
ordinary mock-mirage simulation at 20 km

Target at 20 km: distortion but no mirage

Here we see that stronger refraction in the inversion layer has bent down the ray at −5′ apparent altitude at the observer. All the rays below it are also bent down, so that the lower part of the target is displaced upward, but not strongly deformed.

The upper part of the target, above the inversion, is seen through air with the standard lapse rate. So it's neither strongly displaced nor distorted.

However, the part of the target within the inversion layer is squeezed into a thinner interval of apparent altitude. That's the part between 30 and 50 m height, or the 10% of the 200 m-high target between 15% and 25% of its total height — see the little vertical jog in the transfer curve, near −4′ altitude. This zone of the target displays the effect called stooping (i.e., vertical compression).

This is an obvious consequence of the continuity of the image: the top is hardly displaced, while the bottom is raised; so the part in between has to be compressed.

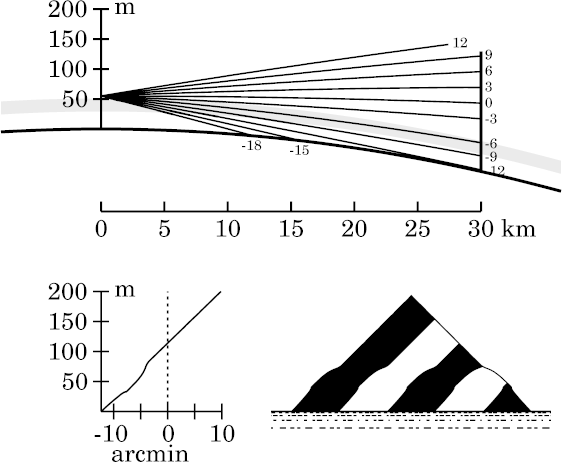
ordinary mock-mirage simulation at 30 km

Target at 30 km: a transition at the horizon

At 30 km, the target is close to the apparent horizon. Now its distortions become more complex. In addition to the squashed zone, there's a zone of vertical stretching, or towering.

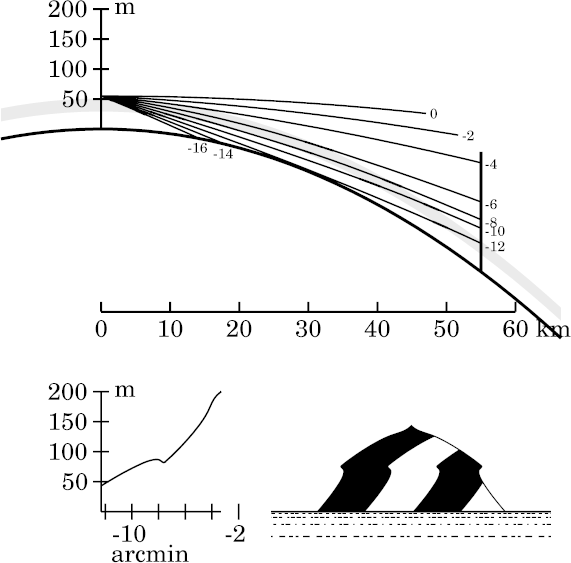
First, note that the stooped zone (the steeper section of the transfer curve) is now much larger. This is the shoulder-shaped feature in the simulated image, produced by the larger deflection of rays near the top of the inversion. (Look at the gap that has developed between the rays the observer sees at altitudes of −3′ and −6′.)

But just below this, at about −8′, there's a zone where the sloping side of the target is imaged as a nearly-vertical line (the short horizontal feature in the transfer curve). If you look at the ray diagram, that's caused by the convergence of the rays between −6′ and −9′ at the target: a tiny piece of the target near 30 m height has been expanded in the image, producing a short, steep cliff. The rather sharp, pointy corner at the top of this cliff is produced where rays just graze the bottom of the inversion.

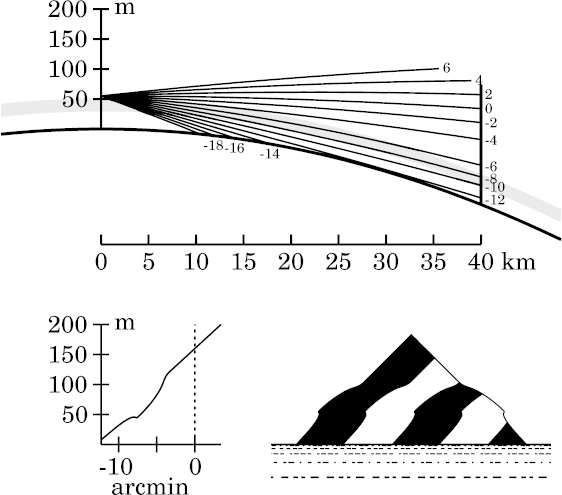
ordinary mock-mirage simulation at 40 km

Target at 40 km: a weak mock mirage

At 40 km, the target is well beyond the apparent horizon. And here we begin to see an inverted image, produced by ray-crossings near 35 km. (Unfortunately, they're too slight to be shown on a ray diagram at this scale.)

In the transfer curve, the flat spot near −8′ in the previous example has become a local maximum, so that features on the target near 45 m height are now seen at two different apparent altitudes near −8′: an erect image below, and an inverted image above.

In fact, if you trace a horizontal line across the transfer curve near 45 m height, you find that it intersects the curve again in the strongly-stooped region, near −6′. So there's a third, erect image above the inverted one. These two images meet at the overhanging lip on the edge of the cliff.

The mock mirage here is not well developed; less than 1′ of the image is inverted. This probably would escape notice with the naked eye, though the general image distortion should be noticed by anyone familiar with the normal view of the scene.

ordinary mock-mirage simulation at 55 km

Target at 55 km: stronger mock mirage

As the target recedes, the inverted (miraged) part of the image becomes more obvious. The lowest parts of the target are disappearing behind the curve of the Earth. (Notice that the dark triangle at the lower right corner of the target in the previous image is now hidden.)

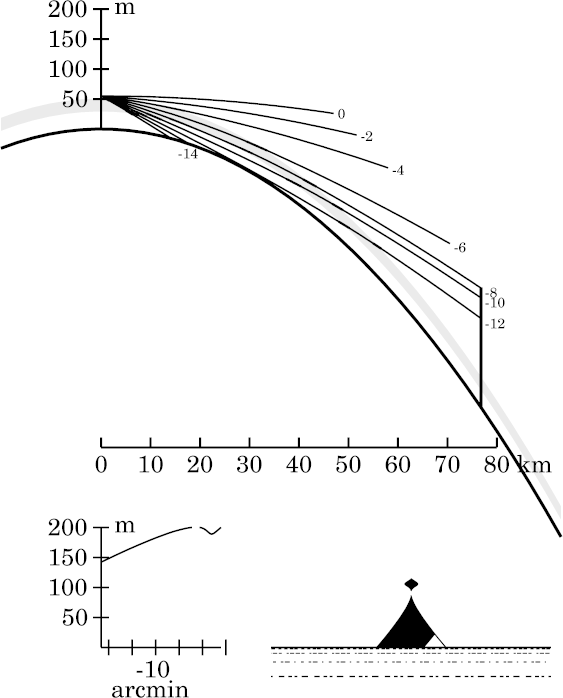
Here, at 55 km, the whole upper section of the target has been stooped down nearly into a sort of shield, or mushroom cap, above the miraged part. (This stooped feature, due to refraction at the top of the inversion, is discussed in more detail here). The little cusp on top is all that remains of the undistorted image seen above the inversion.

Also, notice that the top of the inverted image is vertically compressed, compared to the erect portion below it (look at the slopes of the sides). Of course, its lower part, where it joins the erect one, is vertically stretched.

ordinary mock-mirage simulation at 76.8 km

Target at 76.8 km: obvious mock mirage

When the target is far enough away that the inverted image of its top is separate from the erect image below it, the three images of the tip are obvious. Here we see the appearance at that stage. As the width of the inverted zone of the image is about 2′ here, it should be quite visible to the unaided eye.

As in the previous two cases (target at 40 and 55 km), the mock mirage is produced near an altitude of −8′, where the visual ray grazes the bottom of the inversion.

The upper two images (the erect one above, the inverted one below it) appear together as if suspended in the air. The gap between the inverted image and the lower erect image corresponds to the gap in the transfer curve. This space contains a double image (the lower part erect, the upper part inverted) of a narrow strip of sky just above the top of the target.

Of course, this is the situation that produces little double images of the green rim in mock-miraged sunsets, where the separated piece of rim produces a mock-mirage green flash.

Back to the . . .
introduction to mock-mirage simulations

or the introduction to all mirage simulations

or the main mirage page

or the GF home page

or the website overview page