Introduction to the Mirage Simulations

The Target

A mirage is an image of something ; so before making simulations of mirages, you have to decide on what object is to be miraged. (This isn't a problem with sunset mirages, where the object is necessarily the Sun.)

To simplify the work, the object should have a simple shape. I've chosen a triangle with a 90° vertex at the top, so that the sides slope at 45°. In addition, I've painted some stripes on the triangle parallel to its left edge; these are sometimes useful in distinguishing inverted and erect portions of the miraged images. Although one occasionally sees conical hills with a triangular profile, they don't have stripes; so I'll call my object a “target”, to emphasize its artificiality.

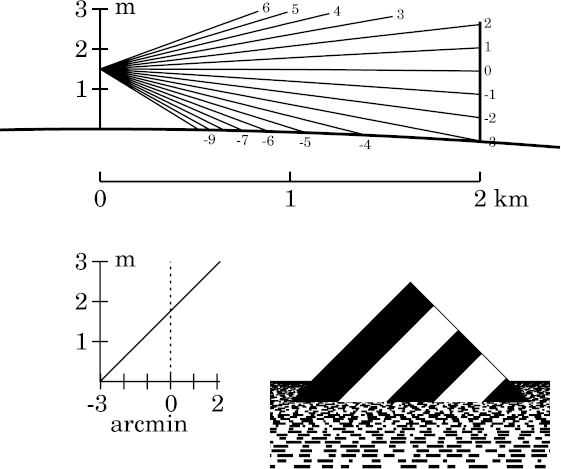Target seen from 1.5 m through 2 km of Std. Atm. To understand mirages, it's very useful to know what the scene looks like without a mirage. So here's a simulation of the target's appearance as seen from a height of 1.5 m through just 2 km of the Standard Atmosphere. This is essentially an undistorted view of the target.

Parts of the diagram

Each drawing in these simulations contains three parts: a ray diagram, a transfer curve, and a simulated image of the target.

The ray diagram

At the top of the simulation is the ray diagram, showing a fan of rays that enter the observer's eye, at the left edge. (Here the rays are practically straight.) The right end of each ray is marked with its apparent altitude at the observer, in minutes of arc.

The vertical scale, at the left side, is height in the atmosphere. You can read off the observer's height by noticing where on this scale the rays all converge. The horizontal scale is horizontal distance; the plot is correct in rectangular coordinates, so the heavy line that represents the Earth's surface is concave downward. Obviously, the ray diagram is grossly exaggerated in the vertical direction, to make its details visible. (Note that the vertical scale is in meters, and the horizontal one, in km.) The target here has twice the height of the observer's eye; this puts the middle of the target at eye level.

The transfer curve

Below the ray diagram, and to the left of the simulated image, is a simple transfer curve that shows height at the target (the vertical scale) as a function of altitude at the observer. As expected, this curve is a straight line of (effectively) unit slope: the image is not distorted. The vertical dotted line in this plot marks the astronomical horizon.

Notice that the vertical scales on the transfer curve and the ray diagram are identical. However, the target is at the right side of the ray diagram; as the vertical scale of the transfer curve has its zero level at the surface of the Earth, which is lower in the ray diagram at the target than at the observer, this is offset from the vertical coordinate of the ray diagram.

The simulated image

The image of the target itself has been scaled to fit in the lower right corner. The Earth's surface is represented as covered with irregular but equally-spaced rulings parallel to the horizon — much as the surface of the sea might appear, with waves parallel to the shore.

In the example shown, it's clear that the target is much closer than the sea horizon, which is seen in the distance behind it. The target resembles a triangular island rising from the sea. The overall effect is not very realistic, but is suggestive enough to give an impression of what the atmosphere might do (in this case, nothing) to the appearance of a simple object.

The Simulations

Simulations of some common mirage types are available at the links below:

inferior mirages;

and, for comparison, terrestrial refraction in the Standard Atmosphere under similar circumstances;

mock mirages, both

ordinary, and

ducted;

and

superior mirages.

In addition, there are simulations of looming, towering, sinking and stooping, although these related refraction phenomena are not themselves mirages.

Notice that the size of the target changes from one set of simulations to the next. For the inferior-mirage simulations, the observer is close to the surface; the apparent horizon is not far away; and a small target, only 3 m high, is used, to make the mirage effects plain. (The same small target is used in the Standard-Atmosphere and looming simulations.) But for the mirages that involve ducts, like the mock mirage and superior-mirage simulations, a much larger target height (200 m) is appropriate.

Making the simulations

To make a mirage simulation, it's necessary to use a model of the lower atmosphere to trace rays between the eye of the observer and the target. The procedure is much like making sunset simulations: start with a temperature profile, from which you calculate a density profile, using hydrostatic equilibrium to determine the pressure at each level; from the density, calculate a refractivity profile; use that to trace rays backward from the observer to the target, using the relationship between ray bending and the refractivity gradient.

The relation between the angular altitude of each ray at the eye to its height at the target is the transfer curve for the mirage. Given the transfer curve, it's easy to draw the apparent distorted shape of the target seen through the refracting atmosphere.

As with the sunset simulations, I have a program that generates the output drawing as a PostScript figure. I then convert that to a PNG file for the appropriate Web page.

Finding your way around in the simulations

Because there are many pages here dealing with mirage simulations, and it's often difficult to see how they all fit together, you may find the Mirage section of the Table of Contents helpful.

Back to the . . .
main mirage page

or the GF home page

or the website overview page