To understand atmospheric refraction quantitatively, you have to understand how Snel's Law works in a spherical atmosphere. This requires only the most elementary trigonometry; just the definitions of sines and cosines are enough to let you follow the argument.
To begin with, consider just the geometry of a spherical atmosphere, without refraction. Here's a figure to illustrate this: the big circle centered at C represents the Earth's surface, and the heavy line NPS represents a ray of light coming from a star or the Sun, say, off to the right somewhere in the direction of S. (The plane of the figure is the plane determined by the incoming straight ray NPS and the center of the Earth, C.)
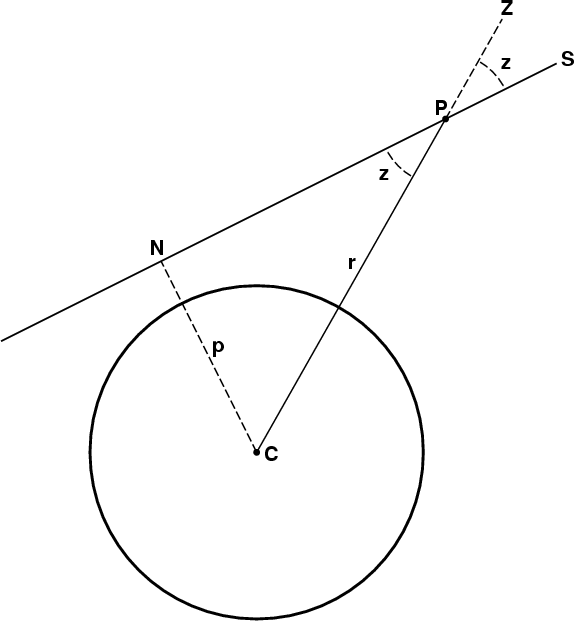The line CPZ is the local vertical passing through some arbitrary point P
on the ray, so that PZ points in the direction of the zenith at P.
You can see that the angle ZPS is the local zenith distance, z,
of the ray at P.
And, because CPZ and NPS are straight lines, the angle CPN is also the
zenith distance z.
Now draw the perpendicular from C to the ray NPS, and assume that N is in fact the foot of this perpendicular, which is drawn as a dashed line in the diagram. (That makes N the nearest point to C on the ray.) The angle CPN is now an angle of the right triangle CPN.
Bearing in mind that the angle CPN is also the zenith distance z of the ray at P, we recall from elementary trigonometry that the ratio of the length of the perpendicular CN (of length p) to the hypotenuse of the triangle, CP (of length r), is just the sine of the opposite angle; that is,
(That's just the definition of the sine of an angle: the opposite side divided by the hypotenuse. You're probably not used to seeing a right triangle turned upside down like this.)
If we clear this of fractions by multiplying both sides by the radial distance, r, from C to P, we have
Notice that this equality holds for every point P along the ray. That is, if P slides back and forth along the (fixed) ray SN, the zenith angle z at P always changes so that the changes in sin z exactly compensate for the changes in radial distance r: their product p remains invariant.
We haven't said anything about refraction yet. This is just basic geometry so far. We might call (r sin z) the geometric invariant, to distinguish it from the refractive invariant we will find later.
Now, let's add a refracting atmosphere to our diagram. We assume it has a horizontal surface — i.e., a sphere concentric with the Earth. So let the dashed circle added in the figure below represent this surface, of radius r1.
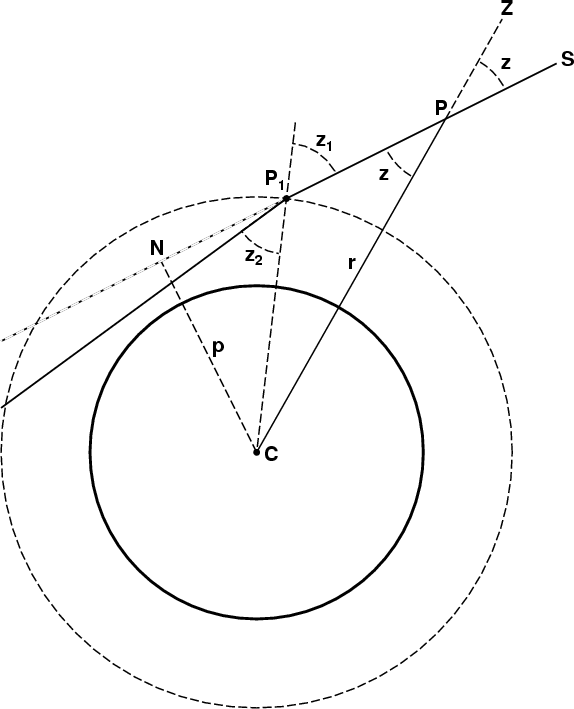
The original ray meets this surface at P1, where it is refracted instead of continuing along the original path (now shown dotted) through N. Because the local vertical at P1 has the direction CP1, which is different from CP, the local zenith distance of the incoming ray is z1 at P1.
For simplicity in calculating the refraction at P1, let us assume Cassini's oversimplified model for the moment: the atmosphere is homogeneous below the refracting surface, and there is vacuum above it. That is, the surface is the “top of the atmosphere” very literally. Then the refractive index on the incident (upper) side of the surface n1 = 1.000 exactly, and the refractive index on the lower side is that of air — call it n2 for convenience.
Now the refractive index of air, n2, is bigger than unity; so Snel's Law tells us that the angle of refraction z2 must be smaller than the angle of incidence z1, because the law of refraction at P1 is just
or
in our particular case, where n1 = 1 exactly.
Now, multiply this last equation by the value of r at P1, which is r1:
From the argument at the end of the previous section, we see that the left side of this equation is just the perpendicular length, p. (The value of the product r sin z is p at every point along the original ray; in particular, it is p at the point P1, so that r1 sin z1 = p .) Therefore, the right side is also equal to p.
This is a remarkable result: even after refraction, the product (n r sin z) is still equal to the length of the original perpendicular, p. That's because the invariance of the product (n sin z) across the refracting surface allows us to replace (n sin z) on the lower side with its value on the upper side, where n was unity.
Furthermore, the geometric invariant applies to the ray after refraction: the product (r sin z) is the same everywhere below P1. And, as the refractive index is also constant throughout the lower layer, the product (n r sin z) is also constant there, and equal to its value p at P1.
Because (n r sin z) is the same everywhere along the refracted ray, and remains invariant even after refraction, we call it the refractive invariant.
Obviously, Cassini's homogeneous atmosphere is not very realistic. We really need to deal with an atmosphere made of many different layers. Suppose, as a start, that we add a second refracting surface below the one considered above. Then the once-refracted ray is refracted a second time when it meets this second interface, at a point we can call P2.
As mentioned above, the geometric invariant applies to the (straight) refracted ray between the first and second surfaces: the value of (r sin z) at every point along the segment P1P2 is constant, and equal to the length of the perpendicular to this straight ray segment from the center, C.
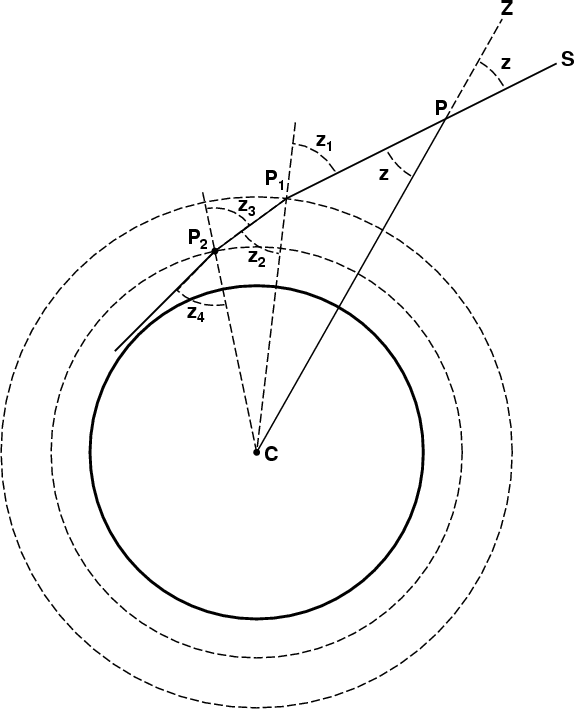
In particular, when the ray meets the second refracting surface at P2, the value of (r sin z) there is the same as its value at P1. This value, of course, is the length of the perpendicular from C to the once-refracted ray P1P2 ; I refrain from adding this line to the diagram, which is already rather cluttered. Let us call this length p1.
But we know (from the result of the previous section) that n1p1 is just p, the length of the original perpendicular CN in vacuum.
Then, applying Snel's Law again at P2 gives
where z3 is the angle of incidence at P2 (from the medium with refractive index n1), and z4 is the angle of refraction into the lowest layer, with refractive index n2. Consequently, multiplying by r2, we have
But the geometric invariant along a straight line allows us to replace r2 sin z3 with the corresponding value of this product at P1, namely p1 = r1 sin z2 . So the left side of this equation becomes n1 r1 sin z2 . And, as we already showed that this equals r1 sin z1 or p, we see that this refractive invariant is still preserved after a second refraction; the right side of the last centered equation is just the value of (n r sin z) after the second refraction.
Clearly, this process can be repeated as many times as we like. No matter how many layers there are, the refractive invariant (n r sin z) remains equal to p in every layer.
We can now extend this process to infinitely many, infinitely thin layers — in other words, to a continuous variation of the refractive index n with height in the atmosphere. The result will always be the same: the refractive invariant is always equal to p, everywhere along the ray:
This fundamental equality is the basis for ray-tracing through any atmospheric model. For the model gives n as a function of r; then the local slope of the ray can be found from sin z.
Those readers who know calculus will see that the path of the ray can be traced if its local slope is known everywhere; differentiating the refractive invariant equation above provides a differential equation from which everything we need can be calculated. But this goes beyond the scope of the present page.
Second, if (nr) is a monotonically increasing function of r, (sin z) = p/nr (and therefore z itself) must decrease monotonically with r; so any ray initially above the horizon approaches the local zenith as we trace it outwards, away from the observer. This means the ray can be nearly horizontal only in the lowest layers of the atmosphere; in the upper atmosphere, the local zenith distance is smaller, and the ray crosses the upper layers more obliquely than the lower ones. So the ray path is less in an upper layer than in a lower one of the same geometric thickness. This is basically why the upper atmosphere has only a very weak effect on refraction: it can never be traversed at grazing incidence.
Let's compare two rays passing through the observer's eye. At the eye, they have different slopes, and so must have different values of the invariant. As the factor (nr) is the same for both rays at any given height, the ray with the larger p must also have a larger value of (sin z): the ray with the steeper slope at the eye remains steeper than the other ray at every other height as well, just as if the rays were straight. So, if both rays are above the astronomical horizon at the observer, the rays diverge as they recede from the eye. That means the rays cannot cross anywhere but at the eye; the image seen is necessarily erect. This result is important for mirages.
We can only get a mirage if a ray is horizontal somewhere along the line of sight, so that r does not change monotonically along the ray. If (nr) is a monotonic function of r, the ray is horizontal at its minimum height above the Earth. Then we see a ray that arrives at the eye from below our astronomical horizon. This is the case for the inferior mirage: the inverted image is always below the astronomical horizon.
Another possibility is that the ray is horizontal at a maximum height. We can see such rays slightly above (though still very near) the astronomical horizon. But for this case, we require that (nr) is not a monotonic function of r; it must have a local maximum. Rays near this maximum can be trapped in a duct. From within the duct, we can see inverted images of distant objects that are also in the duct; this is the classical superior mirage.
Of course, we cannot see celestial objects in the zone at the astronomical horizon that is blocked by the duct. Consequently, mirages of celestial objects — which includes most green flashes — are seen only below the astronomical horizon.
The theorem that inverted images require rays to be horizontal somewhere between the object and the observer, so that only erect images are normally seen above the astronomical horizon (in a horizontally-layered atmosphere) was implied by J. B. Biot in his 1810 monograph on mirages, and explicitly stated in H. W. Brandes's 1814 abridged translation of it into German. It is also explicitly stated by Rudolf Meyer in his 1935 review of refraction and mirage phenomena: “The necessary and sufficient condition for a mirage is the horizontal direction of the ray at some place between beginning and end.” The divergence of rays from the observer above the horizon is very nicely proved by Meyer on pp. 776–777 of his Handbuch der Geophysik article, using essentially the same argument presented here. Meyer states explicitly on p. 800 that inverted images of heavenly bodies are therefore visible only below the horizon.
Because a ray must be horizontal between the observer and the miraged object, only objects beyond the apparent horizon are seen miraged (inverted). (This rule is violated in the common inferior mirages seen on paved roads, because the paving is not perfectly level; all the foregoing discussion assumes a perfectly stratified atmosphere, and this assumption is violated in the surface layer next to a hot, uneven road.)
Where a ray is horizontal, the local value of z is 90°, and sin z = 1. At this point, which must be either a maximum or a minimum in height along the ray, n r = p. This condition makes it easy to find where the ray turns back into layers it has traversed before, if we know its slope at any point along the ray.
This relation suggests that the quantity (n r) as a function of height would be very informative; and indeed, a plot of nr vs. height is the dip diagram, which is discussed in detail elsewhere.
A ray that is horizontal at the edge of a duct is forced to circle the Earth at constant height indefinitely, assuming a horizontally-uniform atmosphere. These circulating rays are discussed on another page.
Copyright © 2002, 2005, 2006, 2009, 2012, 2014 Andrew T. Young
or the
main mirage page
or the GF home page