Inferior-Mirage Simulations

Introduction

Here are some simulations of inferior mirages. The miraged object is my usual triangular target. The observer's eye is 1.5 meters above a warm ocean; this is the view of someone standing at the shoreline. The target has twice the height of the eye (i.e., it's 3 meters high). The model atmosphere used in all the figures below is the same one I've used to simulate Omega sunsets and inferior-mirage green flashes.

Nearby target: no mirage

As usual, the rays here are labelled with their altitudes at the observer. At 1-km range, the 3-meter target subtends 3 milliradians, or about 10 minutes of arc.

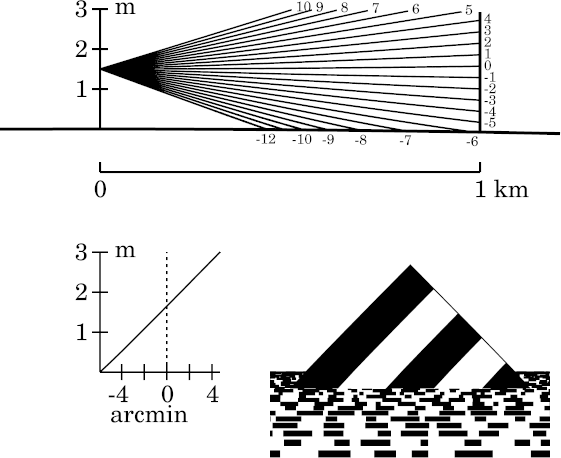
With the target only 1 km away, there's no mirage, because ray curvature is so small that no ray crossing can occur in this short distance. (The smallness of the ray curvature is a direct result of the small curvature of the temperature profile.)

Notice that the transfer curve (in the lower left of the figure) is almost a straight line.

Consequently, the target hardly appears distorted. Notice that it's much closer than the sea horizon, which can be seen behind it in the simulation at the right.

Target near the horizon: slight towering

At 2 km distance, the target is near the apparent horizon (notice that the ray at −4′ is almost parallel to the sea surface near the target). This is much closer than the apparent horizon for the Standard Atmosphere, where the horizon is about 5 km away.

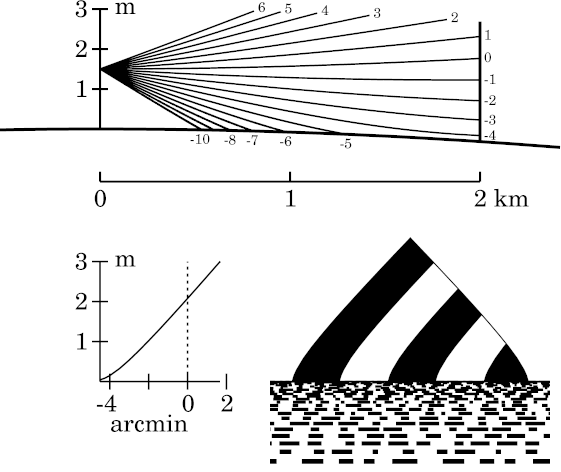
If the lapse rate were constant, we'd expect the target to have half the angular subtense it had at 1 km, which was 10′. Half of 10 is 5; but the actual subtense of the target here is larger: about 6′. That's because differential refraction has stretched the lower part of the target (note the curve at the bottom of the transfer curve, and the corresponding curvature in the lowest parts of the target.) This vertical stretching, or magnification, constitutes towering.

Because the curvature of the temperature profile is marked only near the sea surface, the top of the target still looks fairly normal. Notice that its apex is still very nearly a right angle.

Target beyond the horizon: miraging

At 3 km, the target is appreciably beyond the horizon. That has two consequences: first, the inferior mirage becomes visible at last; and second, the lowest part of the target is hidden below the “fold line” or “vanishing line”: notice that the third black stripe, at the lower right corner of the target in the previous simulations, is no longer visible. This means that less than 80% of the target remains above the sea horizon.

The folding occurs at the minimum in the transfer curve, where the vertical magnification of the image is infinite. The region of large vertical magnification covers more of the target here, so the towering is more pronounced.

The apparent size of the mirage can be measured on the transfer curve, from the vertical axis at the apparent horizon to the minimum in the curve: it's a little less than a minute of arc in extent.

Target far behind the horizon: pronounced miraging and distortion

At 4 km range, the whole target is appreciably stretched vertically; notice how the angle at its apex is quite acute here, while it was still nearly a right angle in the previous simulation. The miraged (inverted) part of the image at the horizon now subtends more than a minute of arc.

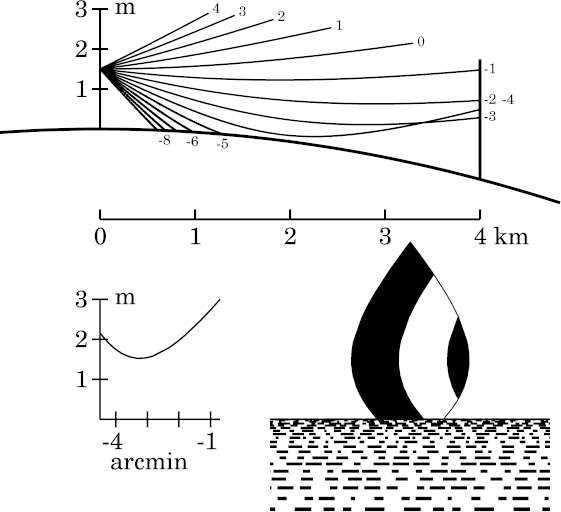
Although the target is now four times as far away as it was at 1 km, where it subtended about 10′ of arc, it remains much larger than the 2.5′ one would expect from simple distance scaling if the whole target were still visible. Actually, you can see from the disappearance of another stripe that only about half of the whole target is still in sight; so the expected height should be only 1.25′. But the apparent height of the target is really almost 4′. The magnification near the fold line makes the image considerably larger than one would expect.

At larger distances, the target rapidly shrinks to a thin vertical feature at the fold line, where it disappears completely at a range between 5.3 and 5.4 km.

While the inferior-mirage atmosphere hides half of the target below the fold line at 4 km range, the Standard Atmosphere allows the target to be more than twice as far away — 9.5 km — before half of it is hidden.

Remember: all the figures above use the same model atmosphere. The differences are just due to changing the distance between the target and the observer.

Back to the . . .
introduction to mirage simulations

or the main mirage page

or the GF home page

or the website overview page