We've already seen an example of the target as seen through the Standard Atmosphere at short range (2 km). These examples won't look very different. However, they do serve to show where the apparent horizon occurs for an observer 1.5 m above the surface with the standard lapse rate.
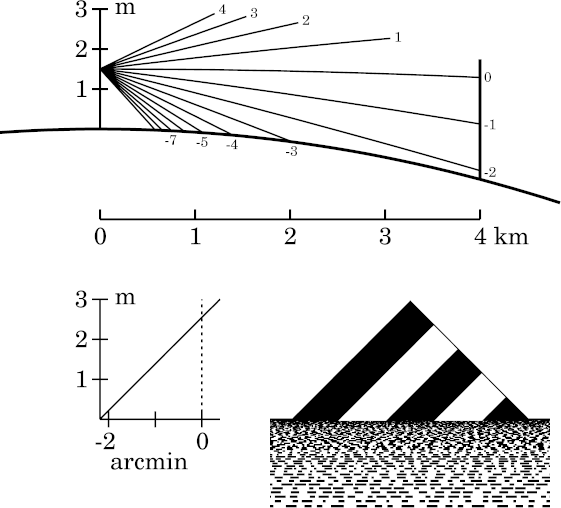
The target subtends about 10′ at 1 km, and 5′ at 2 km, so it's reasonable to expect it to subtend about 2.5′ here, at 4 km. The simulation confirms this: there's negligible distortion.
It isn't clear from the ray diagram that 4 km is closer than the horizon, but the simulated image shows that the base of the target appears just a little lower than the apparent horizon beyond it. (This shows how difficult it is to determine the distance to the horizon accurately.)
Notice that, because the ray curvature is less than the Earth's curvature,
the ray at the astronomical horizon (0′) meets the target
considerably higher than the observer's eye.
The transfer curve shows that this ray meets the target about a
meter above the observer's height.
(This effect is even more obvious in the next image.)
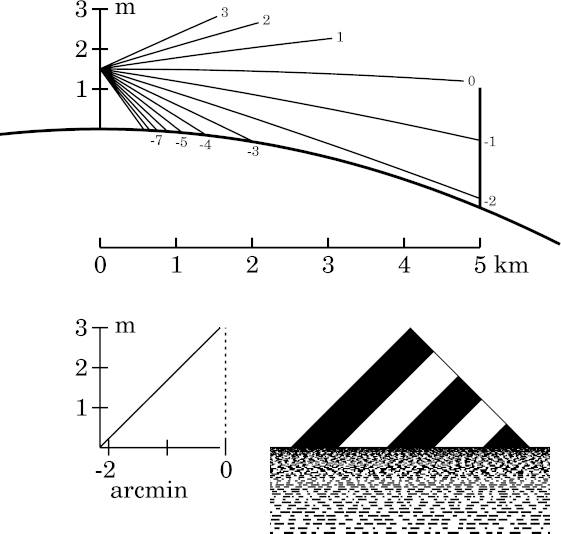
Once again, not very interesting — except to confirm that 5 km is certainly closer to the apparent horizon than 4. (Don't be misled by the ray with an altitude of −2′ at the observer: though it's closest to the surface at about 4.5 km, it's not the actual apparent-horizon ray, which is a little lower.)
Comparing the two simulated images shows the target sitting nicely on the horizon here. And no appreciable part of it is hidden behind the horizon, either (look at the rightmost dark stripe on the target: it's all there.)
Here, the astronomical-horizon ray actually passes above the top of the
target. (Again, the transfer curve shows the effect best.)
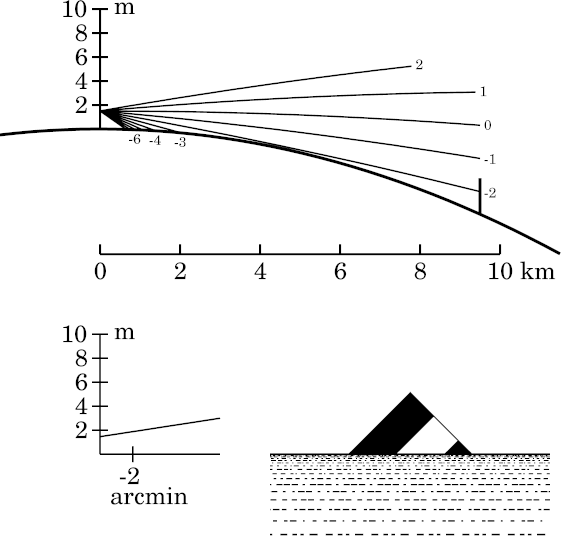
You'll notice that the target is still basically undistorted, in spite of the long air path. Its vertex is still a right angle; there's no obvious vertical stretching or compression.
Copyright © 2008 – 2009, 2012, 2025 Andrew T. Young
or the
main mirage page
or the
GF home page
or the website overview page