Ducts

Introduction

But this has left the information about ducts scattered over many pages. It's useful to have basic information about ducts and ducting in a single location. That's this page, which also has many links to details on other pages. (Remember that links in Italics  refer to the glossary , and that links in boldface refer to the very long bibliography and so may be slow to load.)

A little history

Because wave-optical effects are important at radio and even microwave frequencies, these early observations were compared to propagation in a waveguide — so the word duct  was a natural analogy. Here's a brief explanation from one of the earliest papers on the subject:

In a nonhomogeneous atmosphere whose index of refraction decreases with height, rays of sufficiently small initial elevation angle are refracted downward with a curvature proportional to the rate of decrease of the index of refraction with height. If the radius of curvature is less than the radius of the earth, such rays reach a maximum height and are confined, or trapped , between this height and the earth's surface. This process is referred to as trapping , and the region of the atmosphere within which it occurs is called a duct , because of the analogy with wave-guide propagation.

— M. Katzin, R. W. Bauchman, and W. Binnian
“3- and 9-centimeter propagation in low ocean ducts”
Proceedings of the Institute of Radio Engineers  35, 891–905 (1947)

However, the basic phenomena of ducting were mentioned by Biot (1810 and 1836) and Radau (1882), and discussed in detail by Kummer (1860) and Wegener (1912 and 1918), in the context of atmospheric refraction and mirages — all, of course, without using the term “duct”.

More recently, the word “duct” has been adopted in the optical literature as well [cf. the Meinels' (1984) book review].

How ducting works

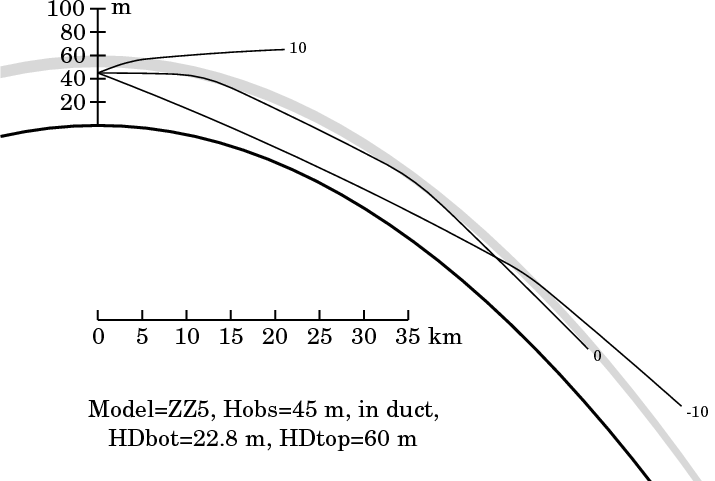The diagram at the left shows this example. The heavy curved line represents the surface of the Earth. Just the lowest 100 m of the atmosphere are shown (see the scale at the upper left of the diagram), with a vertical exaggeration of about 100× (see the horizontal scale of kilometers). The shaded band above the Earth's surface represents the thermal inversion  of 5° between 50 and 60 m height.

Three rays are traced in this model atmosphere, from the position of an observer placed 45 m above the ground, on the height scale at the left. The right end of each ray is marked with the ray's angular altitude  at the observer in minutes of arc: 0 for the ray at the observer's astronomical horizon , and rays 10′ above and below it.

Notice that the rays at 10′ and −10′ are refracted inside the shaded inversion layer, but pass completely through it. However, the horizon ray is quickly bent back down when it enters the inversion, so that it returns to its original height (45 m) after about 24 km. Then the pattern repeats: the ray again enters the inversion and is bent back down near 36 km; it again returns to the original height near 48 km; and so on. This ray is trapped , or ducted.

This ducted horizon ray has most of its path below  the inversion layer, which means that the bottom of the duct is lower than the bottom of the inversion. (The bottom of the duct is discussed in detail below.)

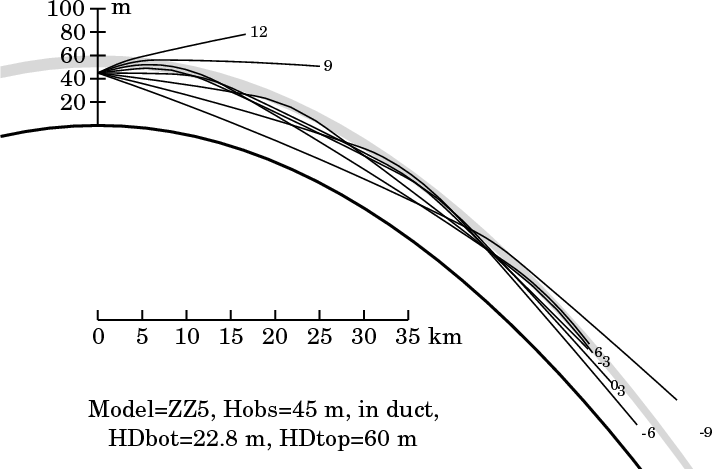Clearly, even rays with a considerable slope — though somewhat less than 10′ — can also be bent back into the region below the inversion layer, and trapped there. The diagram at the right shows rays at 3′ intervals in altitude, for the same observer and model atmosphere as before. While the rays at +12′ and ±9′ pass through the inversion, those with slopes of 3′ and 6′ at the observer are trapped, or ducted.

You can see that the rays 6′ from the observer's horizon (which peak near 8 and 35 km from the observer) penetrate farther into the inversion — i.e., closer to its upper surface — than those only 3′ from it. (e.g., the −3′ ray, whose apex is near 23 km).

Also, notice how the ducted rays all come together about 44 km from the observer. The duct acts like a lens, focusing these rays into a crude image at this distance. This focusing effect produces the vertical exaggeration of images in superior mirages. (When the focusing is sharp, the greatly extended vertical images of objects near the exact imaging distance form the striated zone of the Fata Morgana.)

Depth of the duct

This question is answered in the labels on these diagrams: the top of the duct is the top of the inversion, at 60 m; but the bottom of the duct is far below  the 50-m base of the inversion — it's at 22.8 m for this model atmosphere. (Wegener called the difference between the heights of the top and bottom of the duct its “effective depth” in his 1918 paper.)

The base of the duct can be found from the atmospheric model: it's the height at which the product nR  (where n  is the index of refraction  of air, and R  is distance from the center of curvature of the atmosphere) has the same value as at the top of the inversion. The product nR  is the refractive invariant for horizontal rays at each height; a plot of these values against height gives the dip diagram.

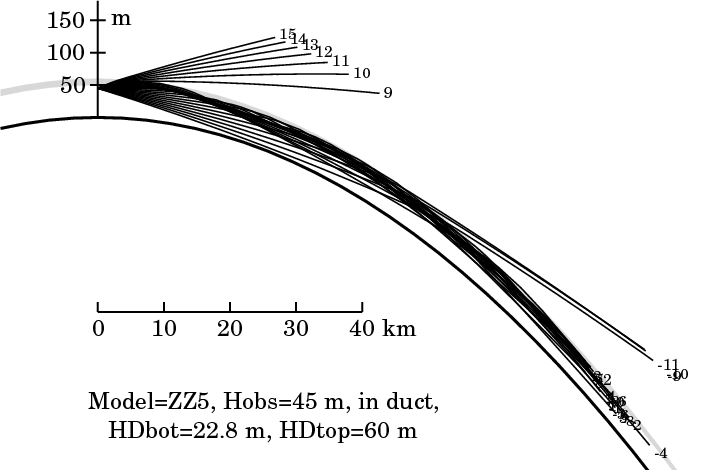It's instructive to plot rays for every minute of arc in altitude at the observer; that's the diagram at the left here, which shows the lowest 180 meters of the atmosphere. You can see three groups of rays: (1) those with altitudes at the observer of 9′ and more, which pass through the inversion without trapping; (2) those that lie within 8′ of the observer's astronomical horizon, which are all trapped in the duct; and (3) those at least 9′ below  the horizon — here, the rays at −9′, −10′, and −11′, which initially pass below the inversion, approach the ground, but then pass back up through the inversion without being trapped. (Rays 12′ or more below the horizon strike the Earth's surface within about 24 km of the observer, and are not shown.)

The ducted rays gradually get out of step with one another, and fill up the duct. You can see this beginning to happen in the right half of the present diagram. (Compare the 22.8-m height of the bottom of the duct with the height of the lowest rays in this region.) The lowest level reached by a ducted ray is the bottom of the duct.

Finally, notice the big gap above the inversion between the two groups of rays that pass up through the duct. This is a region that's invisible from the observer's position. If a radar transmitter were where our observer is, it couldn't illuminate targets in this gap; so radar operators call this region a “shadow zone”. Optically, it corresponds to the zone of sky blocked by Wegener's blank strip.

Inversions and ducts

Also, notice that an optical duct always requires an inversion to produce it, because the optical refractivity of air depends on its temperature. But the reverse is not true: that is, not  every inversion produces a duct. The lapse rate of the inversion must exceed a certain critical value (which is readily calculated) to produce enough bending to trap rays. This critical value is typically about −11°C per hundred meters, for average conditions in moderate latitudes near sea level.

That is, the air temperature must increase with height at a rate greater than 0.11° per meter to produce a duct. That doesn't sound like much; and in fact, such inversions occur quite often in the lower atmosphere. Such an inversion is sometimes called “super-refracting”, because the curvature of a horizontal ray in it exceeds the curvature of the Earth.

Elevated and surface-based ducts

There's a little more discussion of elevated and surface-based ducts on the anomalous horizons page.

Differences between optical and radio ducts

Consequently, while the optical refractivity of air depends mostly on the temperature profile, the radio refractivity depends mostly on the absolute humidity profile. As the amount of water vapor decreases with height much more rapidly than the density of the atmosphere in general, the radio refractivity gradient is typically about twice as strong as the optical one. So, while the curvature of visible light is typically about 1/6 that of the Earth's surface, the curvature of radar beams is about 1/3 that of the Earth. This means that radio waves need less deviation from average conditions to produce a duct, compared to visible light.

Besides differences in refractivity, and the greater importance of wave-optical effects at radio frequencies, one should be aware of another significant difference between the behavior of radio waves and light: the ocean absorbs most of the light that strikes it; but it reflects radio waves. So, while radio waves can travel for thousands of kilometers in a surface-based duct, the analogous optical structure produces a superior mirage of the sea surface only a few kilometers away from the observer. It can also produce a “false horizon” with negative dip — i.e., what Hasse (1960; 1964) called a Kimmfläche  or “horizon surface”. (This is just the upper edge of Wegener's blank strip when the lower edge is hidden by the apparent horizon ). However, when the low-Sun glitter path is miraged in this way, spectacular images can be produced (use that link to see one, in a video by Mila Zinkova). This phenomenon, a Fata Morgana of the sea surface, is discussed in detail by Siebren van der Werf in his 2017 paper.

More details

Summary: What's a duct?

Copyright © 2009 – 2014, 2019, 2020, 2022 Andrew T. Young

or the introduction to mirages

or the Overview page