 The observer is at the right edge of the plot, where n is about
1.000273. The “top of the atmosphere” is at the left edge, where
n → 1.
The values plotted here extend up to only 120 km, where the
refractivity of air is quite negligible.
The observer is at the right edge of the plot, where n is about
1.000273. The “top of the atmosphere” is at the left edge, where
n → 1.
The values plotted here extend up to only 120 km, where the
refractivity of air is quite negligible.
The differential of refraction is
so the refraction integral is
but it's more convenient to get rid of the minus sign by interchanging the limits of integration, thus making the upper limit larger than the lower:
By the way, notice that the refractivity (n − 1) is almost exactly proportional to the density, ρ, so that d(n − 1) ∝ dρ; but d(n − 1) = dn. This makes the independent variable n a linear function of atmospheric density. And, as the temperature varies by less than a factor of 2 through the atmosphere, n is also almost a linear function of pressure.
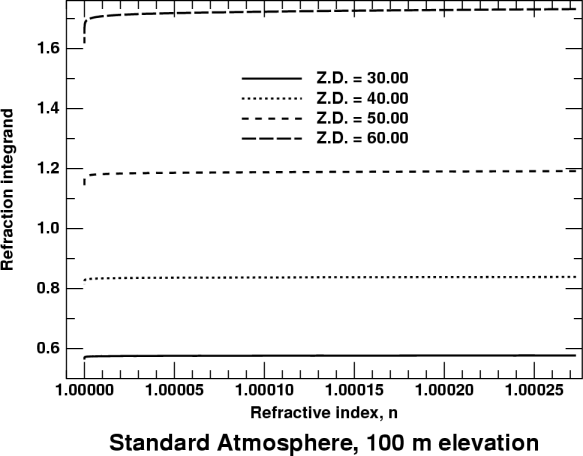
Here's the integrand, (tan z)/n, plotted as a function of n, for apparent zenith distances of 30, 40, 50, and 60°. The observer is 100 meters above sea level; the wavelength of observation is 700 nm. (These values make the curves fit nicely into the graphs, as well as being reasonably typical of actual conditions.)
 The observer is at the right edge of the plot, where n is about
1.000273. The “top of the atmosphere” is at the left edge, where
n → 1.
The values plotted here extend up to only 120 km, where the
refractivity of air is quite negligible.
The observer is at the right edge of the plot, where n is about
1.000273. The “top of the atmosphere” is at the left edge, where
n → 1.
The values plotted here extend up to only 120 km, where the
refractivity of air is quite negligible.
At small zenith distances, like 30°, the integrand is nearly constant up to a height of about 100 km. Both tan z and n are nearly constant up to this height: tan z is nearly constant at the value it has at the observer, because the ray is nearly straight and not far from vertical, so it meets all atmospheric layers at nearly the same angle; and n varies only from 1.000000 to 1.000273 or so. Furthermore, tan z and n both increase slightly across the plot from left to right, so their quotient is more nearly constant through the atmosphere than is either factor separately. So equal masses of air contribute nearly equally to the refraction, regardless of their heights above the ground.
Of course, at very great heights, z eventually becomes appreciably smaller, and so does its tangent. But their values decrease only after n has become indistinguishable from unity. So the ultimate dropoff in tan z is unable to affect the value of the integral. (See the sharp little corner at the left end of the 30° line in the plot.)
We can simplify the problem greatly for small zenith distances by noting that tan z is practically constant along the ray, so that an average value can be taken out of the integrand. Then the integral of dn/n from 1 to n just gives ln n at the observer; or, nearly enough, the familiar (n−1) factor.
A suitable average value of tan z is the value of the local zenith distance at the height h of the homogeneous atmosphere. For small zenith distances, we can adopt the approximations sin z ≈ z ≈ tan z, and replace the sines with tangents in the geometric relation
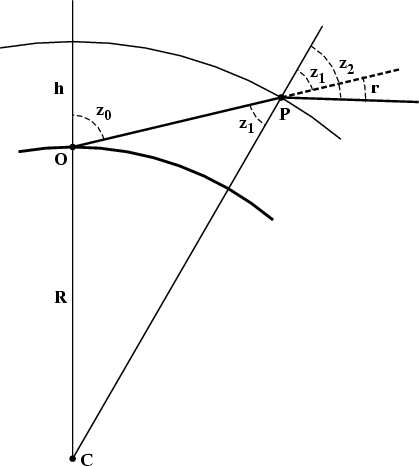 where z0 is the zenith distance at the observer, and
z1 is the zenith distance at height h in the
atmosphere (see the diagram at the right, borrowed from the
page where this is derived.)
So, instead of the equation with sines (shown a few lines above), we write
where z0 is the zenith distance at the observer, and
z1 is the zenith distance at height h in the
atmosphere (see the diagram at the right, borrowed from the
page where this is derived.)
So, instead of the equation with sines (shown a few lines above), we write
In the simpler notation used above, z1 is the zenith distance that appears in the integrand, and z0 is the value of z at the observer. So this last equation is the average value of tan z removed from the refraction integral.
It will be tidier to set h/R = s, so that the factor [R/(R+h)] = 1/(1+s) . Then the average value of tan z is (tan z)/(1+s); and, as the remaining function of n integrated to just (n−1), the refraction is just
This is evidently the same as the formula for refraction in the flat-Earth model, except for the factor of (1+s) in the denominator. [Note that s = h/R is very small, about 0.0013; so this is a fairly small effect.]
Another way to look at this result is that, at small zenith distances, the refraction is the same as for a curved but homogeneous atmosphere. Of course, that's exactly the model used by Cassini; so it's hardly surprising that the Cassini model works well at small zenith distances. And, as Cassini's model does not employ the small-angle approximation used to derive this approximate result, we should expect Cassini's formula to be better than this one — as it is.
However, even this simple tangent approximation isn't too bad. Here's a table to show its errors:
| Z.D. (deg.) | Refraction (arcsec) | tangent formula | error | Z.D. (deg) | Refraction (arcsec) | tangent formula | error | |
|---|---|---|---|---|---|---|---|---|
| 42.2 | 51.42 | 51.47 | 0.05 | 76.8 | 238.1 | 243.1 | 5. | |
| 48.8 | 64.79 | 64.89 | 0.10 | 79.6 | 299.5 | 309.5 | 10. | |
| 55.2 | 81.62 | 81.82 | 0.20 | 81.8 | 376.4 | 396.4 | 20. | |
| 62.9 | 110.74 | 111.24 | 0.50 | 83.0 | 429.7 | 459.7 | 30. | |
| 68.0 | 139.49 | 140.49 | 1.00 | 84.6 | 538. | 598. | 60. | |
| 72.3 | 175.65 | 177.65 | 2.00 | 85.9 | 670. | 790. | 120 |
The simple tangent formula is good enough to be used in correcting precise observations only within 35° or 40° of the zenith, though it's still good enough to use for telescope control and other rough corrections out to about 70° or 75°. Of course, near the horizon, the tangent formula is wildly off. And it's always larger than the true refraction, even where it's nearly correct.
 Here's the plot of the integrand again for the small and moderate zenith
distances. This time, we'll concentrate on the upper curves, particularly
the one for 60° Z.D. (Use the upper edge of the frame for
comparison.)
Here's the plot of the integrand again for the small and moderate zenith
distances. This time, we'll concentrate on the upper curves, particularly
the one for 60° Z.D. (Use the upper edge of the frame for
comparison.)
At moderate zenith distances, like 60°, there is a small but significant decrease of tan z with height (i.e., from right to left in the diagram). This isn't properly accounted for by the crude approximation used above for small zenith distances.
Traditionally, the method used to handle this problem was to write tan z in terms of sin z:
and then expand the square root in the denominator, using the binomial theorem.
The problem with this technique is that even adding a second term, which involves tan3z, doesn't produce a result as accurate as Cassini's simple model. So one must either go to still higher-order terms — not an enticing prospect, as the series turns out to be only semi-convergent — or re-cast the problem entirely.
As Cassini's model provides more than enough accuracy for any practical purpose out to 74° Z.D., my recommendation is to use it, and forget about the series approximations entirely. Just be sure to use accurate values for the refractivity of air, and the height of the homogeneous atmosphere, calculated from the local temperature and pressure.
What about the part of the sky where Cassini's model runs into difficulties?
Here's the integrand, plotted as a function of n, for apparent zenith distances of 70, 75, 80, and 85°:
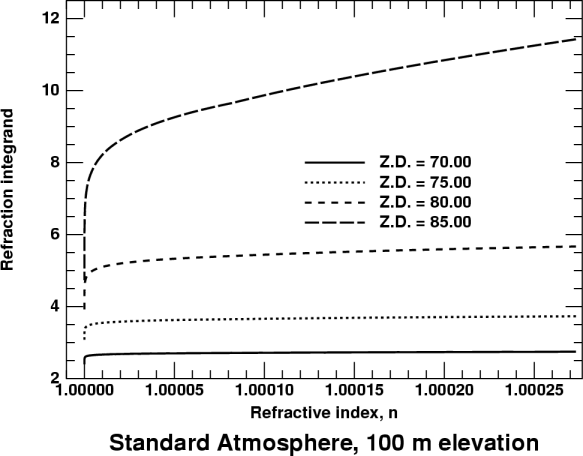 Here you can see two things starting to happen. First, the rounding off
of the corner near n = 1 is becoming quite significant.
(This is due to the large change in z1 in the upper
atmosphere.) Second, the other end of the curve, near
n = n0, is increasingly sloped as
z increases. (This is due to the rapid change in tan z
as z approaches 90°.)
Here you can see two things starting to happen. First, the rounding off
of the corner near n = 1 is becoming quite significant.
(This is due to the large change in z1 in the upper
atmosphere.) Second, the other end of the curve, near
n = n0, is increasingly sloped as
z increases. (This is due to the rapid change in tan z
as z approaches 90°.)
As a result, the refraction integral is influenced more and more by the lowest part of the atmosphere (at the right side of the plot) as we look closer and closer to the horizon. Now the change in tan z through the atmosphere is becoming the most important consideration; we are seeing the transition from ordinary atmospheric refraction, which depends only on the density of air at the observer, to the low-altitude regime in which the detailed structure of the lowest levels becomes important.
Even the structure of the upper atmosphere is beginning to have some influence. You can see a very slight kink in the uppermost curve (for 85° Z.D.) at n = 1.00008: this is due to the change in lapse rate at the tropopause. Such details show that we are out of the region in which Oriani's theorem is valid. Now the refraction depends on the structure of the whole atmosphere — though the parts nearest the observer are still the most important.
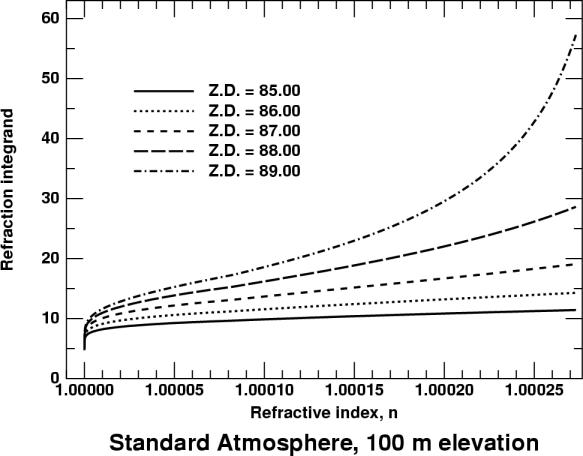 Now take at look at the integrand for a few angles close to the horizon.
Here the refraction is completely dominated by the lowest levels in the
atmosphere (at the right side).
Notice that the lowest levels contribute more and more as the observer's
line of sight approaches the horizon. But the contribution of the upper
atmosphere, at the left side of the plot, hardly increases at all in the
last few degrees.
Now take at look at the integrand for a few angles close to the horizon.
Here the refraction is completely dominated by the lowest levels in the
atmosphere (at the right side).
Notice that the lowest levels contribute more and more as the observer's
line of sight approaches the horizon. But the contribution of the upper
atmosphere, at the left side of the plot, hardly increases at all in the
last few degrees.
This is readily explained by Wegener's principle: if you separate the upper and lower atmospheres, the angle of incidence on the lower surface of the upper part reaches an extremum at the horizon, and changes much less than the inclination of the ray at the observer. This effect is responsible for the breakdown of Cassini's model near the horizon; we may now regard this defect as due to Cassini's total neglect of refraction in the lower layers of the atmosphere, which (as the plot here shows) completely dominate the refraction near the horizon.
Indeed, the near-horizontal refraction is perhaps better understood in terms of the bending of the rays. If you apply Wegener's principle, think of the lower atmosphere in terms of bending, and then regard the upper atmosphere as adding a nearly constant contribution that depends only weakly on apparent zenith distance, you can make sense of the refraction near the horizon.
Actually calculating the low-altitude refraction is more difficult. Because the tangent function goes to infinity at 90°, the integrand of the refraction integral blows up at the observer's horizon. We know the integral itself remains finite — at least for ordinary conditions — but the evaluation of the integral is best handled by transforming to a different independent variable. This is the strategy invented by Biot, and rediscovered by Auer and Standish.
Bear in mind that practical application of these formulae requires attention to the actual circumstances of use and the accuracy required. In particular, the refractivity of air must be calculated accurately for the local pressure and temperature, and the actual effective wavelength of observation.
An often overlooked problem is to measure the humidity accurately, and to use accurate formulae for the effects of water vapor on both the refractivity and the molecular weight of air, which affects the height of the homogeneous atmosphere when Cassini's model is used. The measurement problems are discussed by Stone.
Note that the approximate formula used in NAO 63 (and recommended on pp. 142–143 of the Explanatory Supplement) to convert relative humidity to water mixing ratio is not sufficiently accurate for the most precise work. See Siebren van der Werf's 2003 paper for a better treatment of the water-vapor effects.
Copyright © 2003 – 2006, 2012, 2013, 2017 Andrew T. Young
or the
astronomical refraction page
or the
GF home page
or the Overview page