Cassini's model works amazingly well over most of the sky, but fails rather spectacularly at the horizon. Here are its errors for the Standard Atmosphere, at a wavelength of 700 nm (the values are in seconds of arc):
| Z.D. | Refraction | Cassini | error | Z.D. | Refraction | Cassini | error | |
|---|---|---|---|---|---|---|---|---|
| 60° | 98.051 | 98.049 | 0.002 | 82° | 383.118 | 381.887 | 1.231 | |
| 65° | 121.175 | 121.169 | 0.006 | 84° | 494.371 | 490.313 | 4.057 | |
| 70° | 154.720 | 154.702 | 0.018 | 86° | 684.208 | 666.447 | 17.761 | |
| 74° | 195.367 | 195.316 | 0.051 | 88° | 1058.06 | 947.692 | 110.37 | |
| 76° | 223.712 | 223.615 | 0.097 | 89° | 1399.69 | 1098.01 | 301.68 | |
| 78° | 260.701 | 260.502 | 0.199 | 90° | 1960.13 | 1166.62 | 793.51 | |
| 80° | 310.987 | 310.528 | 0.459 |
For zenith distances less than about 74°, Cassini's model is good enough to be used for the most exacting astrometric observations. From there to about 85°, it remains good to a few seconds of arc — certainly good enough for use in telescope pointing. But at the horizon, the error exceeds 13 minutes of arc.
Another way of looking at this is to calculate the relative error, which is less than 1% out to 84° Z.D., but jumps to more than 40% at 90°. Why does Cassini's model fail so catastrophically just within a few degrees of the horizon?
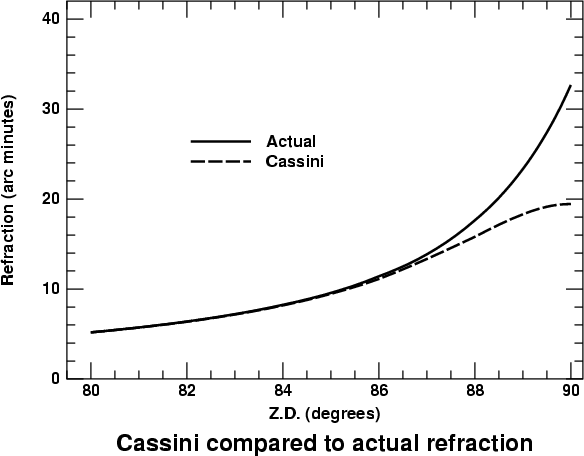
The nature of the problem is shown more clearly by graphing the two functions. Here they are, plotted for the last 10 degrees above the horizon:

Obviously, the curve for Cassini's model turns over and becomes flat at the horizon, instead of becoming steeper as the actual refraction does.
This defect is much more obvious from the plot than it was in the tabular data. But Cassini's contemporaries even noticed it in his refraction table, which had one-degree intervals: the difference of his last two entries was smaller than between the values for 88 and 89 degrees. In a letter of Cassini's, he even says that Riccioli had asked whether this was a typographical error. (Cassini insisted that his table was correct.)
The reason for the flattening is evident from symmetry considerations, if one is willing to think of an observer elevated above the Earth's surface, so that the apparent horizon lies below the astronomical one. Then it is obvious that two lines of sight at equal angles above and below the horizontal meet Cassini's refracting surface at the top of the atmosphere at the same angle of incidence, and must therefore suffer identical refractions. This makes Cassini's refraction symmetrical about the astronomical horizon; it must have an extremum there, and consequently a horizontal tangent.
This can be regarded as an example of Wegener's principle, if we regard the two regions (in Cassini's model) as the atmosphere and the void above it. Indeed, Wegener's 1912 paper contains diagrams illustrating exactly this symmetry — though without reference to Cassini's model. (In Wegener's case, the refracting surface is a strong thermal inversion rather than the top of the atmosphere.) His Abb. 3 shows a pair of rays symmetrically disposed about the horizontal, and the accompanying text on p. 29 explicitly states that they have the same angle of incidence on the refracting surface.
A different (but equivalent) way of looking at the failure of the Cassini model at the horizon is to notice that the homogeneous atmosphere assumed by Cassini actually corresponds to air in hydrostatic equilibrium, but only if the lapse rate is about 34°/km (see the calculation on the ray-bending page). This is more than 3 times the adiabatic lapse rate; such an atmosphere would be dynamically unstable. From the point of view of Biot's magnification theorem, one could say that the homogeneous atmosphere necessarily has unit magnification at the astronomical horizon; therefore, its refraction must be locally constant there — as was shown in the figure above.
From this point of view, the failure of the Cassini model at the horizon is due to its unrealistic lapse rate. But this becomes apparent only near the horizon, where the temperature gradient becomes the dominant factor determining the refraction. At greater altitudes, the effect of lapse rate rapidly becomes negligible, and Cassini's model gives good results.
Copyright © 2003 – 2006, 2013 Andrew T. Young
or the astronomical refraction page
or the
overview page