Mirages Produced by a Zigzag Temperature Profile:

Effects of Target Distance

Introduction

Although the most spectacular variations in these mirages are those due to changing the height of the eye, there are also some interesting effects due to changing the distance to the target. These effects for that same model (a 2° inversion between 50 and 60 m, shown by a gray band in the ray diagrams) are displayed on this page. Remember that the duct actually extends below this band.

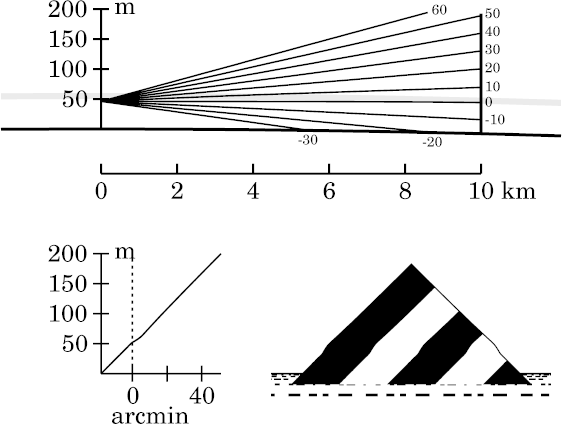
Because of the great importance of eye height, what you see depends very much on where you stand. So I'll consider a couple of different heights: one just inside the bottom of the duct, at 46 m height; the often-used height of 54 m, near the middle of the duct; and perhaps more to come.

Eye height: 46 m

Let's begin just above the bottom of the duct, but below the bottom of the thermal inversion that produces it.

200m target seen at 10km in ZZ2 model from 46m ht.

Target at 10 km, eye at 46 m (zigzag model)

We can safely skip the demonstration that at ranges of just a few kilometers, the target is seen essentially undistorted. So here's its appearance at a distance of 10 km. Even at this range, the distortion is very slight.

The transfer curve shows that the slight towering is confined to a few minutes of arc above the astronomical horizon. This raises the upper part of the image, which therefore displays a slight looming effect, but is undistorted.

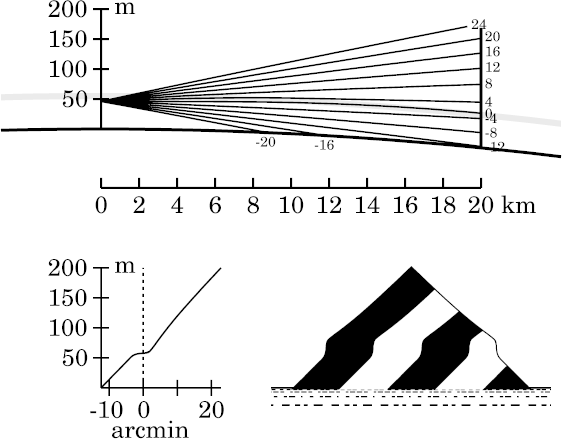
200m target seen at 20km in ZZ2 model from 46m ht.

Target at 20 km, eye at 46 m (zigzag model)

Here we have the same image that is discussed on the page where eye-height effects are shown. The main effect is exaggerated towering in the vertically stretched zone of the target, which is nearly centered on the astronomical horizon (see the transfer curve). The top of the image looms more than at 10 km.

A slight stooping of the region immediately above the towered zone is barely visible here. There is no mirage at 20 km range; but you can see from the ray diagram that the horizon ray is bending down toward the ray at −4′ altitude, so ray-crossing and mirage are produced at slightly larger target distances.

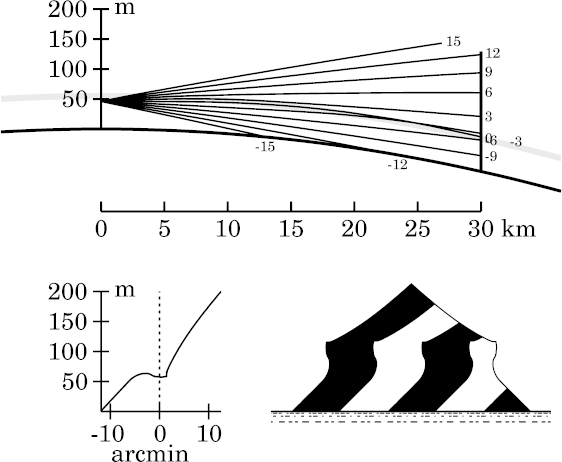
200m target seen at 30km in ZZ2 model from 46m ht.

Target at 30 km, eye at 46 m (zigzag model)

Sure enough, at 30 km range, we have a mirage; note the crossing of the 0′ (horizon) ray and the −3′ ray about 25 km from the observer, near the top of the inversion.

Notice that this mirage has two distinct parts: a strongly towered image in the strip centered on the horizon ray, and a less-towered part in the zone immediately below that. This lower part of the mirage is clearly Wegener's Nachspiegelung, because the strongly-towered zone corresponds to Wegener's miraging strip.

The upper, strongly-towered part of the mirage is produced by rays near the horizon ray, all of which are focused near the same height on the target. They all are ducted, and reach the target within the inversion.

The lower, Nachspiegelung part of the mirage is due to rays near the −3′ ray. Like it, they pass entirely through the inversion (without ducting), and have different path lengths within it, striking the target above the inversion layer.

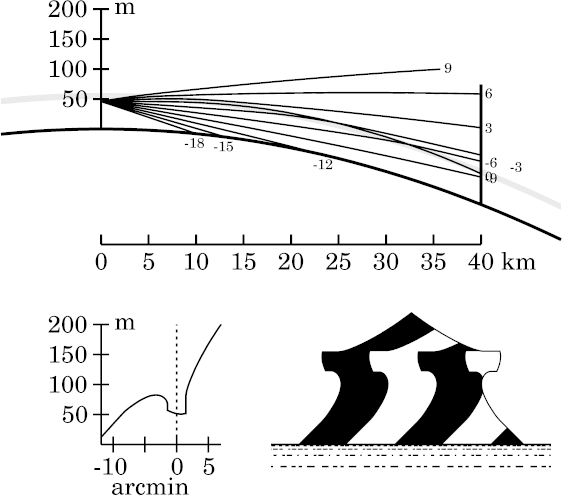
200m target seen at 40km in ZZ2 model from 46m ht.

Target at 40 km, eye at 46 m (zigzag model)

At 40 km, the edges of Wegener's strip are becoming well-marked. As discussed in connection with his toy model, the top of the image is stooped, because its looming decreases rapidly with increasing altitude; notice how far apart the +6′ and +3′ rays are at the target.

This case is discussed in detail on the page dealing with the effects of eye height. As mentioned there, the curvature of the sides of Wegener's strip is due to his periodicity effect, although it is weaker here than for his toy model at the same eye height and target distance. So, while the toy model already produced an erect image in the miraged strip at this geometry, we see only a distorted (curved) inverted image here, in the zigzag model.

However, the effect still works; it just takes a somewhat greater target range to produce focusing, and eventually image erection — as the next two cases demonstrate.

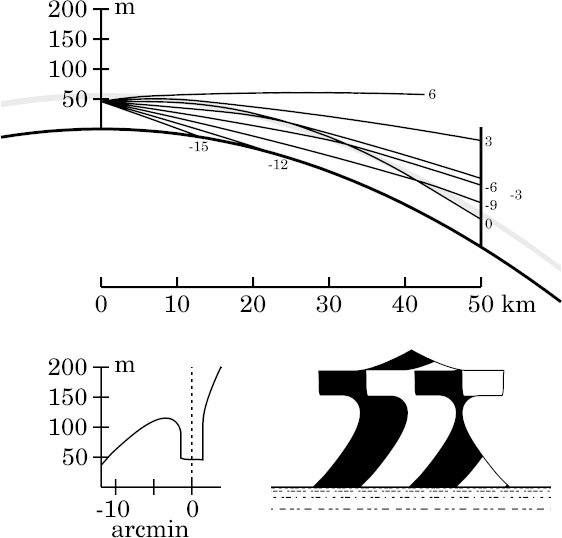
200m target seen at 50km in ZZ2 model from 46m ht.

Target at 50 km, eye at 46 m (zigzag model)

At 50 km, rays near the horizon ray are all focused on the target at a height near the base of the inversion. This region is therefore enormously towered, producing a nearly vertical image in the miraging strip. (Because of its stronger periodicity effect, the toy model reaches this situation only 30 km from the observer.) Here, we are close to the transition from an inverted to an erect image in the miraging strip.

The increasing range produces increased stooping of the top section of the image, above Wegener's strip. The lower part of the image is disappearing below the apparent horizon: we have already lost the rightmost black stripe at the bottom right of the image.

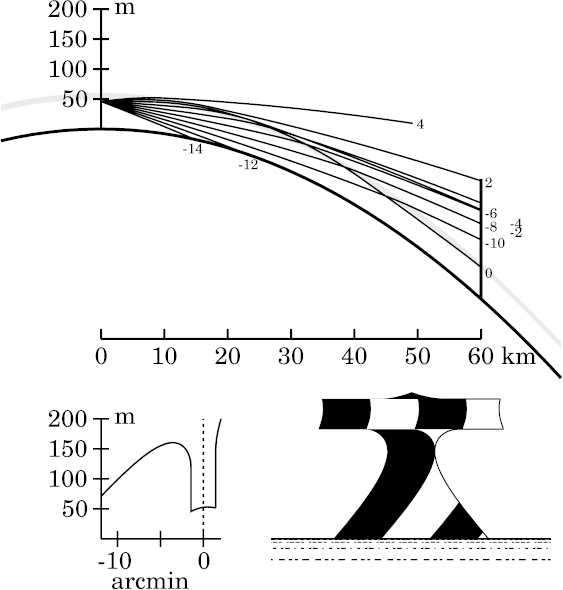
200m target seen at 60km in ZZ2 model from 46m ht.

Target at 60 km, eye at 46 m (zigzag model)

Sure enough, at 60 km, the mirage in Wegener's strip has become an erect image, thanks to the continued operation of the periodicity effect. This image is somewhat comparable to that in the toy model's strip at 40 km.

Of course, the zigzag model produces a much stronger Nachspiegelung below the strip. And the greater range here has lowered all the erect parts outside the strip: now, even the white stripe at the lower right corner has almost sunk below the apparent horizon.

200m target seen at 67km in ZZ2 model from 46m ht.

Target at 67 km, eye at 46 m (zigzag model)

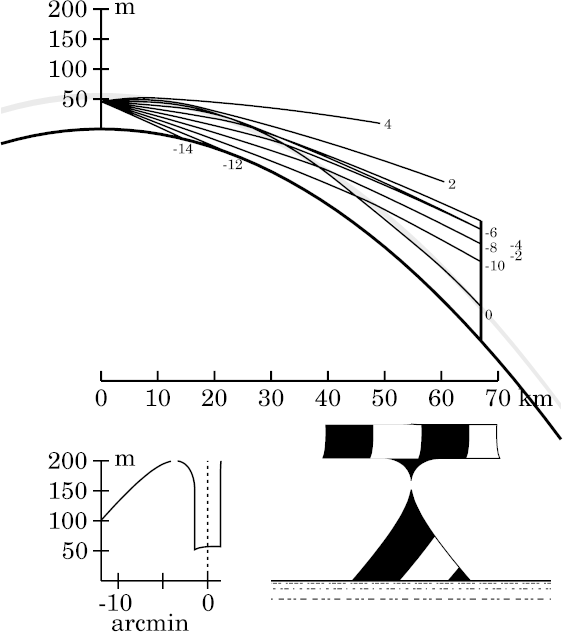
A few kilometers farther away, and the target continues to sink below the apparent horizon. The Nachspiegelung has now separated from the erect image below it; the stooped top has shrunk to almost nothing.

The periodicity effect is continuing to modify the mirage in Wegener's strip: once again, its towering is increasing, as we approach another image inversion.

Eye height: 54 m

Because I've frequently used a height of 54 m with my duct models, I'll show a fairly complete sequence of simulations for different distances using this model and height.

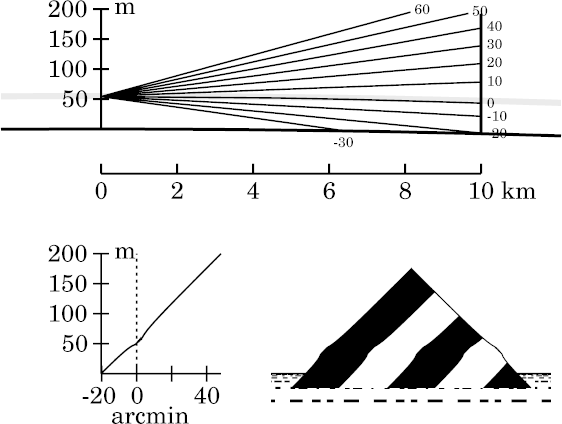
200m target seen at 10km in ZZ2 model from 54m ht.

Target at 10 km, eye at 54 m (zigzag model)

Once again, we'll skip the undistorted view at a few kilometers' range, and start at 10 km.

As you might expect, the small distortion near the astronomical horizon is a little bigger for this observer, near the middle of the thermal inversion, than for the one at 46 m height.

Qualitatively, what we see here, at 54 m, is similar to what was seen at 46 m: slight towering near and above the horizon ray, and slight looming in the upper part of the image. But the effects are too small to make out clearly at this short range.

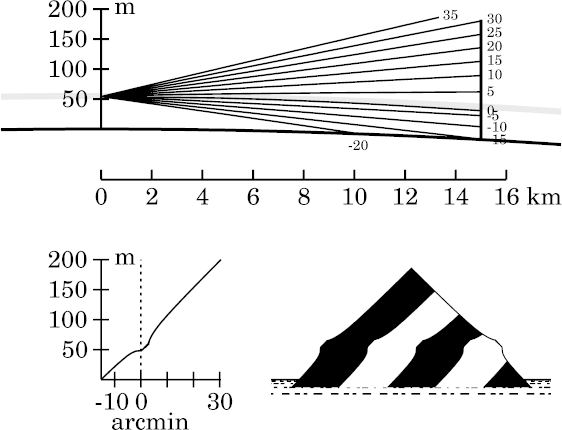
200m target seen at 15km in ZZ2 model from 54m ht.

Target at 15 km, eye at 54 m (zigzag model)

However, at 15 km range, three well-defined image (or transfer-curve) zones are clearly distinct. Rays near and just above the horizon ray (which meets the target near the base of the inversion) are entirely contained in the inversion layer; so they form an undistorted, but somewhat loomed, image. (That's the sloping side of the bumps in the simulated view.)

Below this undistorted zone, the rays leave the inversion layer before reaching the target — the more so, the farther they are below the astronomical horizon. So the looming decreases rapidly with decreasing altitude, producing a vertically stretched (towered) zone.

Above the undistorted zone, the same effect is at work, but in reverse. Again the looming falls of with increasing distance from the horizon, but here that's the direction of increasing altitude. So this region is vertically compressed (i.e., stooped).

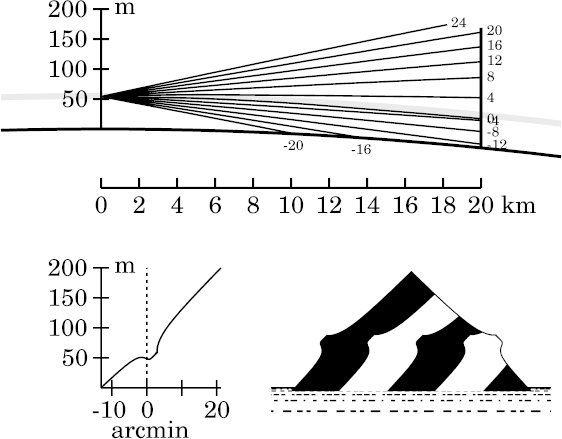
200m target seen at 20km in ZZ2 model from 54m ht.

Target at 20 km, eye at 54 m (zigzag model)

At 20 km, the change in bending with altitude as rays leave the bottom of the inversion is so rapid that the towered zone just below the astronomical horizon has become an inverted image: the superior mirage of textbooks.

The three image zones are still quite prominent: the short, undistorted section (loomed), sandwiched between the stretched — here, miraged — lower zone and the squashed (stooped) one above it.

Because of the longer path in the thermal inversion, the horizon ray actually leaves the bottom of the inversion just before reaching the target; so the boundary between the lower two zones has now moved up to just above the horizon. Thus, the mirage is gradually eating into the undistorted zone from below, as the target distance increases.

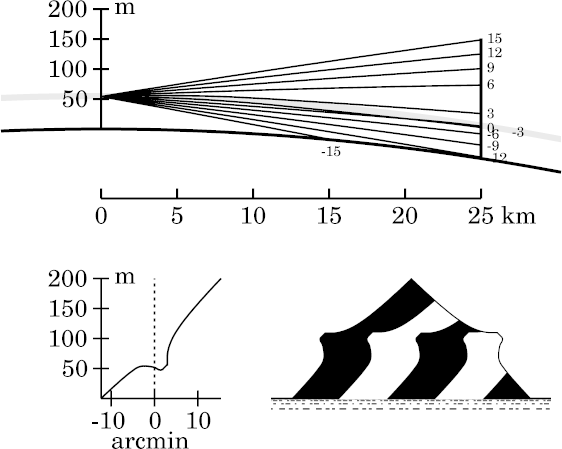
200m target seen at 25km in ZZ2 model from 54m ht.

Target at 25 km, eye at 54 m (zigzag model)

These trends increase rapidly with distance, because the ray displacement due to different ray curvatures increases quadratically with range. Here, at 25 km distance, the inverted mirage image is already considerably larger than at 20 km. The shortening of the undistorted zone is also apparent.

Finally, the stooping of the upper zone has increased, while the apparent altitude of the target's apex has decreased with distance; so the stooping is now evident in the whole upper part of the target (notice that its apex angle is now obviously obtuse).

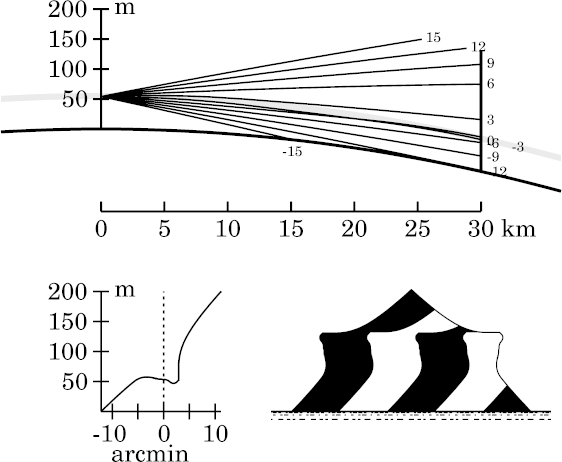
200m target seen at 30km in ZZ2 model from 54m ht.

Target at 30 km, eye at 54 m (zigzag model)

At 30 km, the undistorted zone is reduced to little more than a blunt corner. The inverted image below it is developing additional structure, due to the operation of Wegener's periodicity effect.

Above the projecting corner, the bottom of the stooped zone is becoming the flat upper edge of Wegener's miraging strip. This edge is a discontinuity between trapped (ducted) rays and those that pass freely through the inversion.

Despite the increasing complexity, there are still only three images, at most, of target points. This is a classic 3-image mirage; but if the target had been shorter, so than none of it projected above Wegener's strip, it would be a textbook 2-image superior mirage.

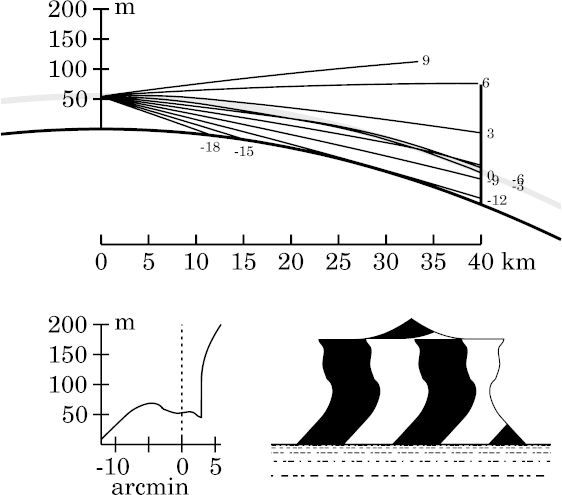
200m target seen at 40km in ZZ2 model from 54m ht.

Target at 40 km, eye at 54 m (zigzag model)

Here the periodicity effect has produced a reversal of slope in the transfer curve near the astronomical horizon. That's the erect (but very towered) zone in the simulated image. This zone now offers 5 images (counting the extremely flattened one on top).

Notice that the undistorted zone that was formerly visible above the miraged zone has disappeared entirely here. It has been replaced by a sharp corner, where the top edge of Wegener's strip is now prominent, just below the very stooped apex of the target.

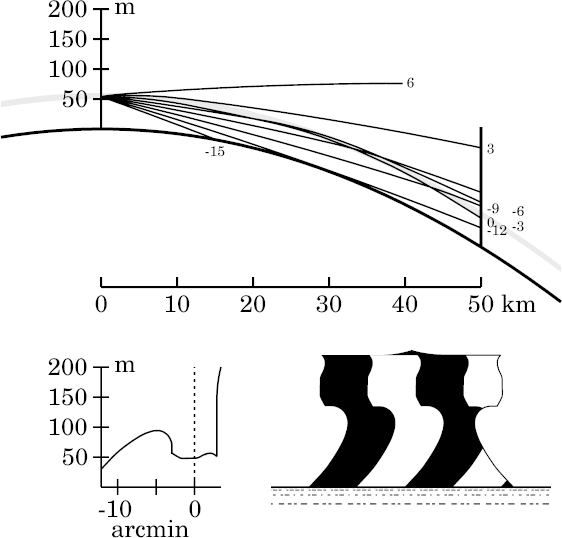
200m target seen at 50km in ZZ2 model from 54m ht.

Target at 50 km, eye at 54 m (zigzag model)

The target is almost twice as far away as the apparent horizon here, and its lower parts are starting to sink below that horizon (see the disappearing dark strip at the lower right corner). At this distance, the bottom edge of Wegener's strip is becoming apparent. The remaining inverted image below this edge is Wegener's Nachspiegelung.

The upper half of the strip contains a prominent erect image, due to ray-crossings near 40 km. The entire strip is filled with highly stretched, multiple images. This would probably be considered a Fata Morgana mirage in the real world.

Only a trace of the extremely stooped apex of the target remains visible.

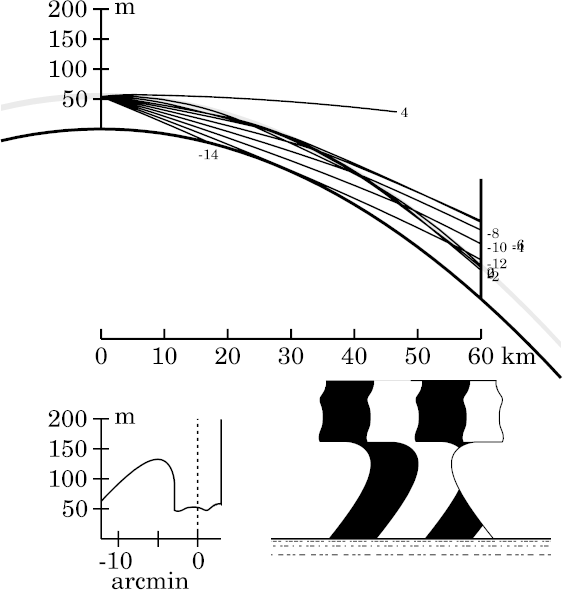
200m target seen at 60km in ZZ2 model from 54m ht.

Target at 60 km, eye at 54 m (zigzag model)

At 60 km, more of the target is disappearing below the horizon, and Wegener's miraging strip is becoming more complex. Below the strip, the Nachspiegelung is obvious.

The top of the target, above Wegener's strip, has practically disappeared.

More realism?

While the zigzag model demonstrates many of the phenomena seen in real mirages, real thermal inversions cannot have the sharp corners of the zigzag profile used here. Heat transfer requires real temperature profiles to be smooth as well as continuous; and the smooth transitions between regions with different lapse rates produce additional effects that are shown on another page.

Back to the . . .
introduction to superior-mirage simulations

or the introduction to all mirage simulations

or the main mirage page

or the GF home page

or the website overview page