Height Effects in Wegener's Superior-Mirage Model

Introduction

As Alfred Wegener points out, in his 1918 paper, the ray at the astronomical horizon of an observer in a duct is reflected at the duct's top more frequently than are the rays at the edges of the “reflecting strip” that contains the superior mirage. The shorter period of the horizon ray, compared to the limiting rays, produces a growing distortion of the superior mirage with increasing distance.

However, Wegener did not use his periodicity effect to explain the effects of varying eye height in superior mirages. Because height of the observer strongly modifies all mirage phenomena, and because Wegener's periodicity principle can be used to explain some eye-height effects, even in realistic model atmospheres, it's worth showing some examples here.

The basic idea is that the discrepancy in periodicity of ducted rays between the edges of Wegener's blank strip and its center (the astronomical horizon) causes the edge or “limiting” rays to fall out of step with those near the (astronomical) horizon, with successive reflections of the rays at Wegener's density discontinuity. So the images of miraged objects become increasingly distorted with distance.

However, as this discrepancy also increases with height above the bottom of the duct, it's apparent that the image distortions in Wegener's model must increase with height of the eye, as well as with distance.

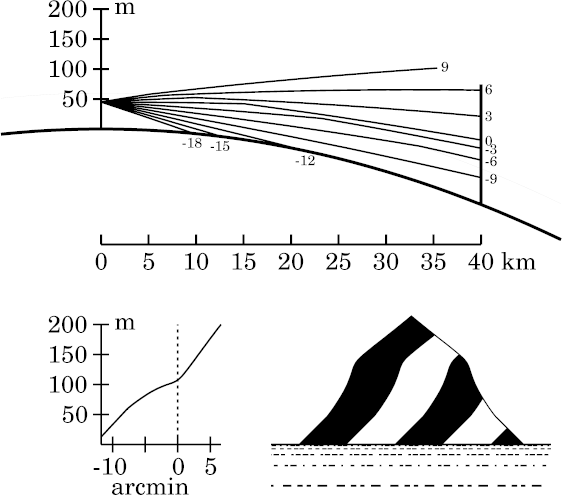
This page illustrates this effect, using the usual 2° temperature discontinuity in Wegener's model to produce the duct, and the 200-m high target I've used for other superior-mirage simulations. The discontinuity is at 60 m height, and the bottom of the duct is just above 45.3 m. I'll start out with a relatively nearby object, 20 km away, and then repeat the exercise for a more distant target, at 40 km. At each target distance, I'll start just below the bottom of the duct and progress upward; the initially simple images gradually become more complex.

Target 20 km from observer

200m target seen at 20km in Weg model from 45m ht.

Eye at 45 m (toy model)

At the left is the simulation for an observer at 45 m height, just below the bottom of the duct. So of course there's no miraging (image inversion). On the other hand, there is an obvious shoulder-shaped distortion of the image, somewhat like what's seen in terrestrial mock mirages, where the observer looks obliquely through the top of an inversion. However, there's an essential difference: in the mock mirage, the distorted zone is stooped, so that the upper part of the image lies below the extrapolation of the lower sides. Here, instead, the distorted zone shows towering: the top of the image lies above the extrapolation of the lower sides.

The distorted zone, of course, lies just at the astronomical horizon, where the line of sight meets Wegener's discontinuity most obliquely. (Notice the kink in the horizon ray about 15 km from the observer, where it is refracted at the discontinuity.)

200m target seen at 20km in Weg model from 45.5m ht.

Eye at 45.5 m (toy model)

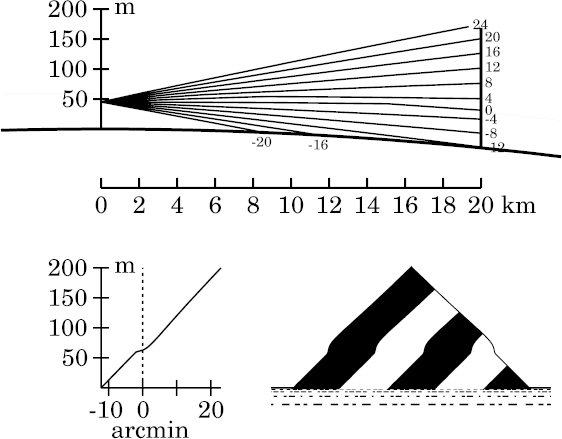
Now let's raise the observer just half a meter, to 45.5 m height. This puts the observer just inside the bottom of the duct, and produces a narrow zone (Wegener's “reflecting strip”) centered on the astronomical horizon, containing an inverted (i.e., miraged) image.

Notice that the horizon ray is now much more strongly deviated than in the previous case, because it is now reflected rather than refracted. It meets the target nearly in the same place as the direct ray 4′ below the astronomical horizon; so the miraged strip of target comes from well below the neighboring erect parts of the image — which accounts for the “ears” on the simulated image. (The slope of the ends of these projections shows that they form an inverted image.)

Caution: The sudden appearance of a sharply delimited miraged strip on entering the duct here results from the unrealistic discontinuity in Wegener's model. Real mirages don't act this way.

200m target seen at 20km in Weg model from 46m ht.

Eye at 46 m (toy model)

Moving up another half meter, we see the rapid widening of the miraged strip in the simulation at the left. The lower edge of the strip is about to merge with the direct image below it.

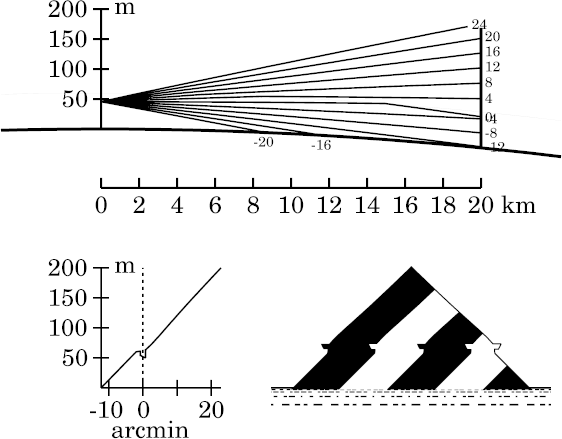
The image inversion in the miraged strip is now more obvious than in the previous example. This is a simple superior mirage of the 2-image type: there are only two images of the miraged zone: the inverted one in the strip, and the erect image of the same features below it. Because the inverted image lies above the erect one, this is a classical superior mirage. (Unfortunately, it's also an unrealistic effect of Wegener's unphysical density discontinuity.)

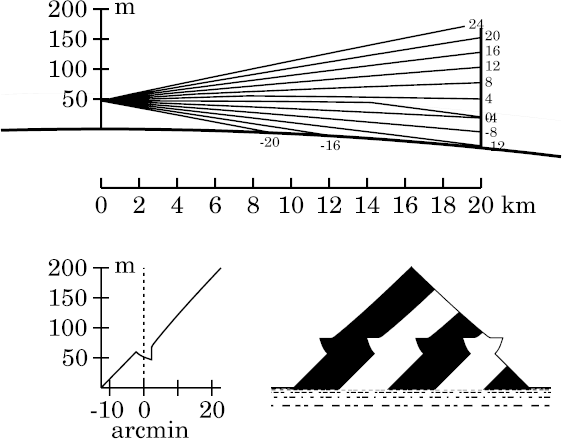
200m target seen at 20km in Weg model from 47m ht.

Eye at 47 m (toy model)

Just one meter higher, at 47 m, the lower edge of the miraged strip has disappeared, because rays that would have encountered it now meet the target before reaching the edge of the strip. For example, the horizon ray (at 0′) and the ray at −4′ now intersect at the target; they did not quite meet when the observer was at 46 m height.

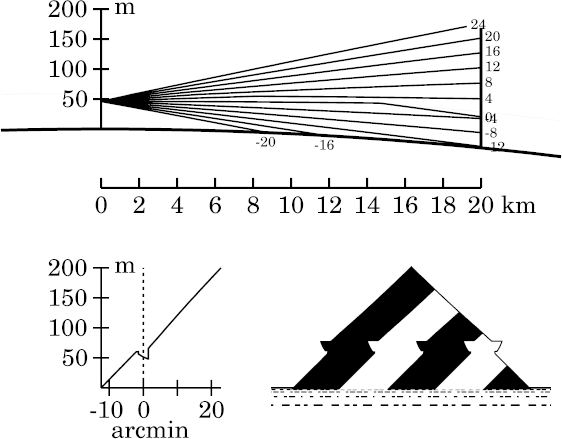
Notice that Wegener's distortion effect is beginning to appear here: the sides of the inverted image are now appreciably curved.

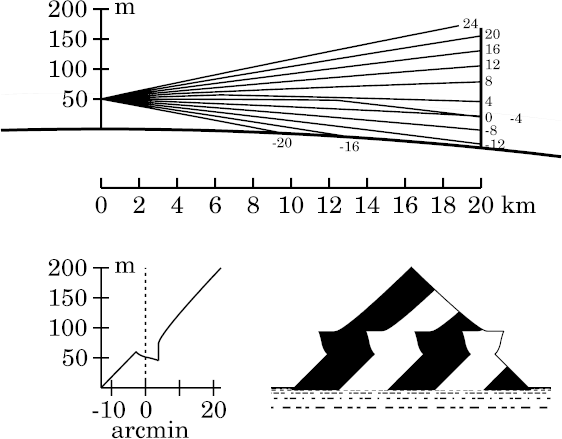
200m target seen at 20km in Weg model from 50m ht.

Eye at 50 m (toy model)

At 50 m, the horizon ray and the −4′ ray intersect before the target. This ray-crossing guarantees an inverted image, of course. The distortion of the inverted image is more pronounced, because the increased height of the eye has also increased the discrepancy in reflection-periods of the horizon and limiting rays.

200m target seen at 20km in Weg model from 54m ht.

Eye at 54 m (toy model)

At 54 m, near the middle of the duct, the miraged strip is wide enough to trap all rays within 4′ of the astronomical horizon. The three rays at altitudes of +4′, 0′, and −4′ are “drawn together like a knot” (to use Wegener's phrase) about 16 km from the observer — or, as an opticist would say, this point is approximately conjugate to the observer's eye. Consequently, the vertical magnification of the inverted image near the astronomical horizon is very large: the transfer curve is almost horizontal, and the simulated image is almost vertical there.

However, there are still only two images of the miraged zone: an inverted (though distorted) one above an erect one. So this would still be interpreted as a simple, 2-image, superior mirage.

200m target seen at 20km in Weg model from 57m ht.

Eye at 57 m (toy model)

A few meters higher yet, and we find that the discrepancy in periods of the horizon and limiting rays has become large enough that additional erect and inverted images have appeared near the horizon. The multiple images would make this display almost a Fata Morgana. The miraged image is becoming more complex as we approach the top of the duct (at 60 m).

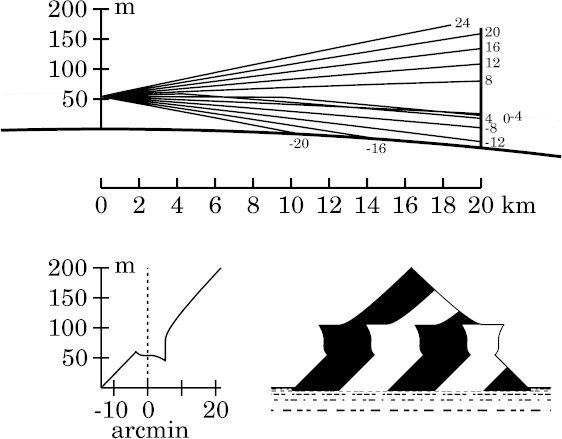
From an optical point of view, the increased foreshortening of the curved reflecting surface (i.e., Wegener's density discontinuity) has shortened its effective focal length, especially near the astronomical horizon. The zonal aberrations of this foreshortened cylindrical mirror would be regarded as the cause of the shorter focal length near the horizon.

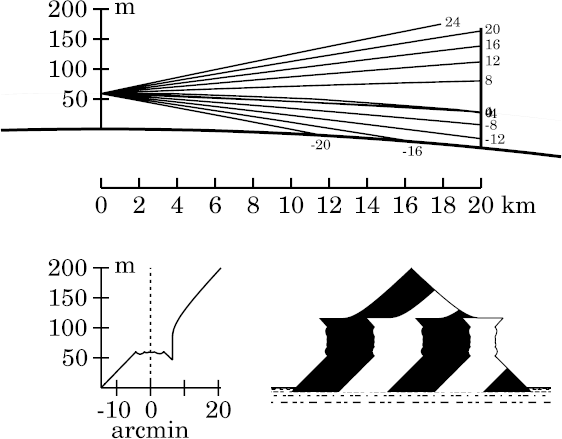
200m target seen at 20km in Weg model from 59m ht.

Eye at 59 m (toy model)

Finally, just 1 meter below Wegener's reflecting density discontinuity, we see multiple reflections of the horizon ray, and multiple images within the miraged zone. Near the astronomical horizon, the imaging is dominated by the rapid variation in effective focal length of the mirror with altitude; so the image is fairly symmetrical about the astronomical horizon.

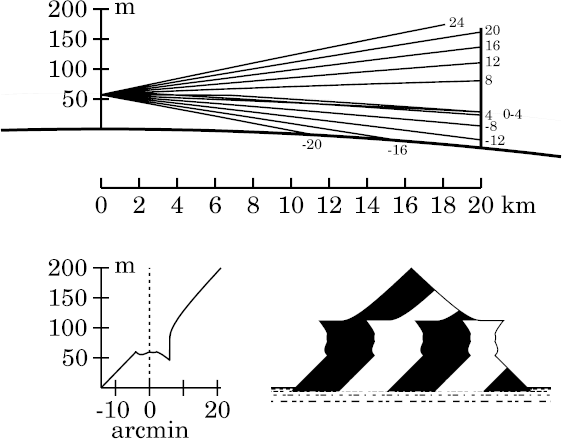
Because of the multiple images and vertical symmetry, this would certainly be regarded as a Fata Morgana display, if it could appear in the real world. Actually, this is just an artifact of Wegener's oversimplified model.

Target 40 km from observer

Now, let's look at a similar series of simulations, but with the target moved twice as far away. The greater target distance makes it subtend a smaller angle, of course; so we'll draw rays for every third minute of altitude, instead of every fourth one.

The increased distance also hides some of the target below the horizon, and makes the miraging strip at the astronomical horizon appear to fall higher up on the target itself. However, the inversion at 60 m height still strikes the target in the same place; so the miraged region contains images of the same part of the target as before.

200m target seen at 40km in Weg model from 45m ht.

Eye at 45 m (toy model)

As at 20 km range, no mirage is visible from just below the bottom of the duct; but there is distortion. However, the curvature of the distorted zone, here at 40 km range, is the reverse of what it was at 20 km. Here the sides of the distorted zone are concave instead of convex; and the steepest part is at the top of the zone, instead of the bottom. There's still towering: the upper part of the image is higher than you'd expect from the lower part, and the distorted zone is stretched vertically — though unevenly.

There's also looming: the middle of the target is raised well above its geometric position by the refraction at Wegener's density discontinuity. And the looming is largest right at the astronomical horizon, where the observer's line of sight meets the discontinuity most obliquely; look at the kink in the horizon ray. But that intersection of the horizon ray with Wegener's density discontinuity occurs only about 15 km from the observer (see the ray diagram for the target at 20 km for a closer view of it).

Below the astronomical horizon, the looming rapidly diminishes, both because the angle of incidence at the refracting discontinuity is decreasing, and also because the refraction takes place much closer to the target. (Notice that the refractive kink in the ray at −3′ is about 23 km from the observer, rather than the 15 km for the horizon ray.) As the refraction occurs closer to the target, there's less path available to displace the ray's intersection at the target. So the looming quickly falls to zero as we look farther below the astronomical horizon.

Above the astronomical horizon, refraction at the discontinuity always occurs relatively close to the observer; so the lever-arm effect of varying distance between the kink in the ray and the target is small. The main effect is a decrease in the refractive displacements because the angle of incidence decreases away from the astronomical horizon. This produces a steady decrease in looming with increasing altitude: a vertical compression, or stooping, of the upper part of the image (notice that the apex of the target has become obtuse, instead of a right angle).

The transfer curve shows that the bottom 30% of the target, which lies entirely below the refracting discontinuity, is essentially undistorted. The next 20% is the part below the astronomical horizon, which shows increasing looming (and therefore, towering) with increasing altitude. The top half of the target is stooped, because the looming is steadily decreasing with altitude above the astronomical horizon.

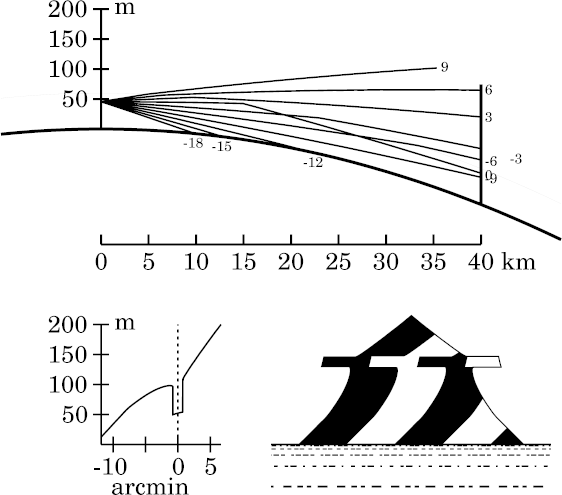
200m target seen at 40km in Weg model from 45.5m ht.

Eye at 45.5 m (toy model)

Here the observer is just above the bottom of the duct. Notice the reflection of the horizon ray where it meets the discontinuity, 15 km from the observer: this reflection produces a much larger deviation of the ray than the grazing-incidence refraction in the previous case.

The miraging strip is now much more pronounced than when the target was 20 km from the observer, because the reflected rays near the horizon have had another 20 km to be deviated, and so strike the target much closer to the ground. Both upper and lower edges of the strip are quite marked here.

But the sloping ends of the miraged image show that it's erect rather than inverted. How can that be?

You can't see it here, because too few rays are shown; but in fact, this is one of those re-inverted inverted images on the far side of a ray-crossing — as described by Wegener. (The ray-crossing that produces the second inversion will become apparent when the miraging strip is wide enough to contain more ducted rays.)

Although this erect image nicely illustrates a feature of Wegener's toy model, it's an unrealistic consequence of Wegener's oversimplified assumption of a discontinuity. If the thermal inversion is represented by a continuous change in temperature, this feature does not occur.

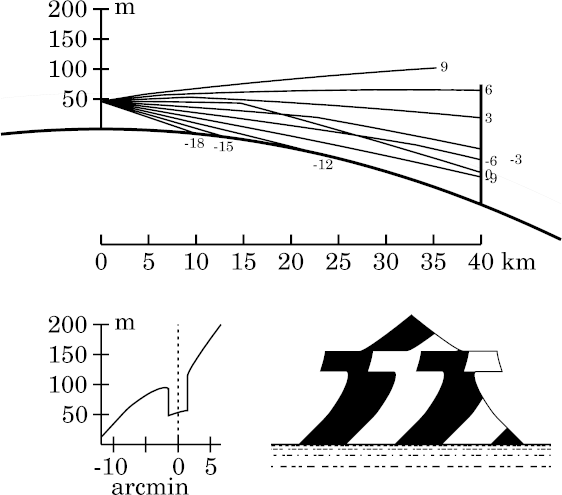
200m target seen at 40km in Weg model from 46m ht.

Eye at 46 m (toy model)

Up another half meter: the miraged strip, with its erect image, is now much wider. A trace of an inverted image is visible just below the strip. This inverted image below the strip is the first sign of Wegener's Nachspiegelung.

Notice how steep the nearly vertical edges are in the miraged strip. As these are images of target features with a 45° slope, the whole strip is strongly affected by towering (vertical stretching), as well as looming (unusual height above the apparent horizon).

The looming/towering/stooping of details just outside the miraging strip are practically the same as they were for an observer below the duct.

Apart from the Nachspiegelung, which is too small to attract attention, this would appear to be a 2-image mirage, with both images erect.

Warning: A more realistic atmospheric model produces a considerably different appearance. Wegener's toy model should not be taken at face value.

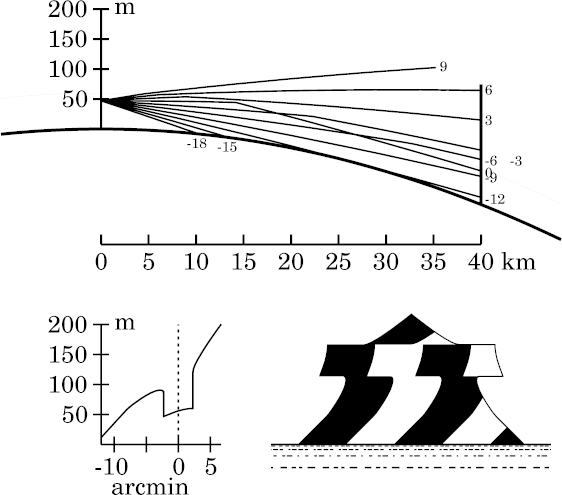
200m target seen at 40km in Weg model from 47m ht.

Eye at 47 m (toy model)

With increasing height above the bottom of the duct, the miraged strip continues to grow wider, and the Nachspiegelung becomes more visible. The ray diagram shows three reflections of ducted rays at Wegener's density discontinuity: the horizon ray, 15 km from the observer; the −3′ ray, at 23 km; and the −6′ ray, at 32 km.

Also, the distortion of the superior mirage in the strip is becoming obvious (notice the curved sides). Once again, this is a result of Wegener's periodicity effect.

Even at this height, the naked eye would probably not notice the Nachspiegelung, and a two-image mirage would be reported. However, this would appear anomalous, as both naked-eye images would be erect. But, once again, a more realistic model behaves differently.

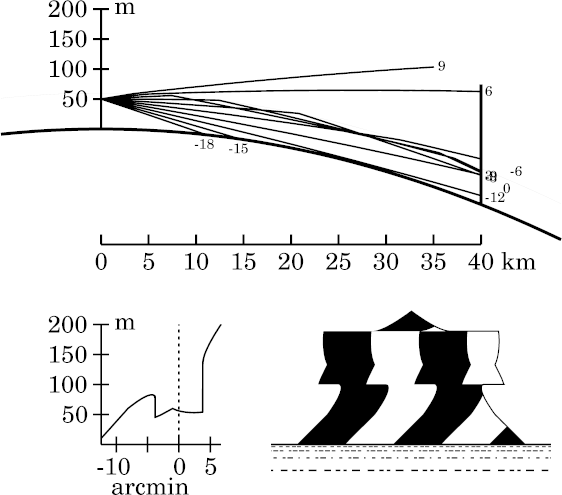
200m target seen at 40km in Weg model from 50m ht.

Eye at 50 m (toy model)

Here, the miraged strip is wide enough that we can see the confluence of the rays at +3′, 0′ (horizon ray), and −3′, about 27 km from the observer. (This is evidently the ray-crossing that produced the erect image noticed just inside the bottom of the duct.)

However, we now have an inverted and highly stretched (towering) image near and above the astronomical horizon. That's evidently due to a second reflection of rays near the astronomical horizon, about 36 km from the observer.

The Nachspiegelung is more obvious than before, and the miraged strip centered on the astronomical horizon is now so wide that it hides most of the distortions that were evident to an observer below the duct.

We have a complex mirage display here that is almost a Fata Morgana, with highly distorted, multiple images. Three images of target features near 50 m height are evident. In contrast, the zigzag model presents a still more complex picture.

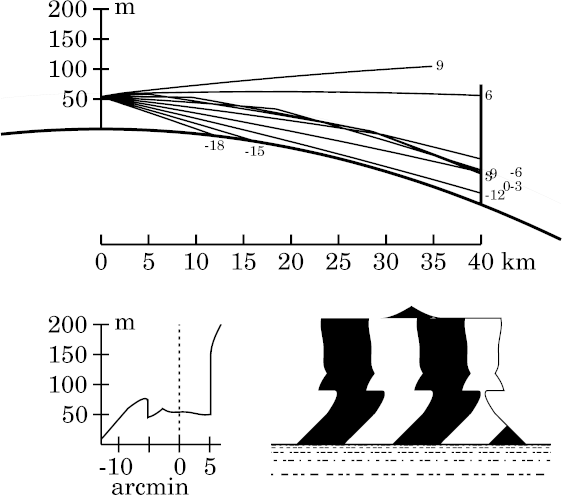
200m target seen at 40km in Weg model from 54m ht.

Eye at 54 m (toy model)

As the observer approaches the top of the duct, the horizon ray approaches grazing incidence at the reflecting discontinuity; and of course the interval between successive reflections of this ray is also decreasing. Here, the second reflection of rays near the horizon occurs only 29 km from the observer. The increasing inequality of the reflection periods of different rays introduces still more distortions in the image.

The width of the miraged strip is just over 10′ here. This would be a fairly spectacular mirage to the naked eye, despite the small temperature jump (2°) that replaces the inversion in Wegener's model.

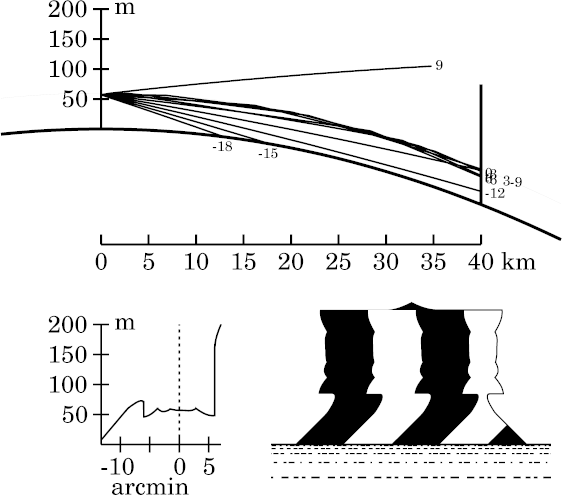
200m target seen at 40km in Weg model from 57m ht.

Eye at 57 m (toy model)

At 57 m, the variation in reflection periods of different rays is becoming very large, so that Wegener's periodicity effect begins to dominate the image structure. The details in the miraged strip are becoming symmetrical about the astronomical horizon.

The strip is now more than 12′ wide, and conceals much of the “direct” image. Five of the traced rays (+6′, +3′, 0′, −3′, and −6′) are ducted. Their many reflections at Wegener's density discontinuity practically outline it.

Features near eye level are multiply imaged; one easily finds 5 or 6 images of some points (draw a horizontal line across the transfer curve, or a vertical line through the simulated image, to match them up). This would probably be considered a Fata Morgana display.

200m target seen at 40km in Weg model from 59m ht.

Eye at 59 m (toy model)

Finally, just a meter below Wegener's density discontinuity, the image has become nearly symmetrical across the whole width (about 14′) of the miraged strip, because of the overwhelming influence of Wegener's periodicity effect. This symmetry, together with the multiple images, would make this display a good example of the Fata Morgana.

Back to the . . .
introduction to Wegener's superior-mirage model

or the introduction to mirage simulations

or the main mirage page

or the GF home page

or the website overview page