Wegener's Periodicity Effect

Introduction

The path of a ducted ray is strictly periodic: it oscillates between two limiting heights, retracing the same shape over and over again (assuming the atmospheric structure does not vary horizontally). This periodicity, and the limiting heights, can be inferred from the dip diagram — which itself is just a consequence of the refractive invariant.

Alfred Wegener noticed that the length of the period (between corresponding parts of the same ray path) depends in a remarkable way on the ray's altitude at the observer. He then used this relationship to give a qualitative explanation of the distortions in superior mirages.

Wegener's relationship can also be used to infer other properties of superior mirages, so it's worth detailed examination.

Wegener's reflection model

Alfred Wegener developed a simple model for mirages and other refraction phenomena, assuming that the thickness of a temperature inversion can be neglected. Collapsing an inversion to zero thickness makes it a density discontinuity. This oversimplified model replaces the actual refraction in the inversion with a fictitious total internal reflection.

Wegener, in his 1918 paper, stated that

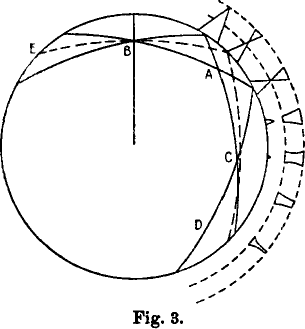… the two points of reflection of the limiting rays at E, A and D must … always be equally far apart, while the reflection point of the horizontal ray is shifted back more at each new reflection. The path of the rays is therefore not exactly symmetric at the reflection point A, and at C only the two limiting rays intersect, while the horizontal ray here runs somewhat above this intersection.

Notice that the two limiting rays — the two solid arcs that intersect at the observer's position, at B — have the same shape; they're just one another's reflections about the vertical line. (This follows from the symmetry properties of refracted rays.)

As I've noted elsewhere, Wegener's figure is a little confusing; so I'll try to explain his idea with simpler diagrams here.

Straight rays

First, let's go back to Wegener's earlier model, presented in his 1912 paper, in which ray curvature is neglected, and the rays are drawn as straight lines, instead of circular arcs. He justifies this approximation as follows:

It's well known that the ray curvature is less than the Earth's curvature. So, to be sure, one would obtain quantitatively false values if one regarded the rays as straight; but qualitatively, the phenomena must occur just the same way. If we imagine a cross-section through the Earth in the plane of the ray, we can without difficulty “stretch” the Earth's surface (i.e., increase the radius of curvature) until the previously curved ray has become straight.

This is a very useful transformation; in fact, all the phenomena depend locally just on the difference of the curvatures of the ray and the Earth, so that subtracting out the ray curvature — which makes the rays straight — is both permissible and convenient.

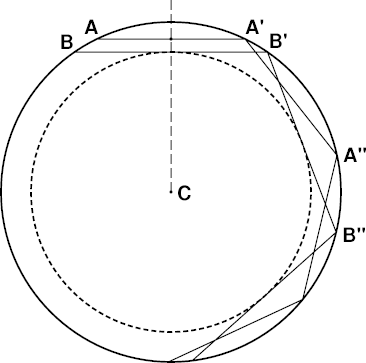simplified Wegener ray-diagram, straight rays So here's Wegener's cross-section through the Earth, with center at C. In my diagram at the left, the outer heavy circle (BAA′B′A″B″…) is Wegener's density discontinuity, and the dashed circle inside it is the bottom of the duct — or, as Wegener described it, the envelope of the limiting rays. The diagram at the left shows two ducted rays, AA′A″… and BB′B″…, with different perigee heights. BB′B″… is one of Wegener's limiting rays, which is just barely trapped in the duct; any ray below BB′ is refracted at Wegener's density discontinuity, instead of being reflected back into the duct.

The lowest point on a ray is its perigee, where it's closest to C. At the perigee point, the ray is locally horizontal (i.e., perpendicular to the local vertical.) The perigee points on the two ray segments AA′ and BB′ are their midpoints, which fall on the dashed vertical line that bisects them. The period of the upper ray is just the interval AA′, or A′A″; and the period of the lower ray is from B to B′ = B′B″.

It should be obvious that the segment AA′ with the higher perigee is shorter than BB′, so that the period of the higher ray is shorter than the period of the lower ray. As BB′ here is a limiting ray, its perigee is lower than that of any other ducted ray, and its period is longer than that of any other ducted ray. Notice that it's horizontal at the bottom of the duct (the heavy dashed circle).

If we imagine an observer placed at the midpoint of AA′ (i.e. its intersection with the dashed vertical), this ray is at the observer's astronomical horizon. But to draw the observer's limiting rays, at the edges of the blank strip, we have to rotate the limiting ray BB′… about the center C until this ray passes through the observer's position.

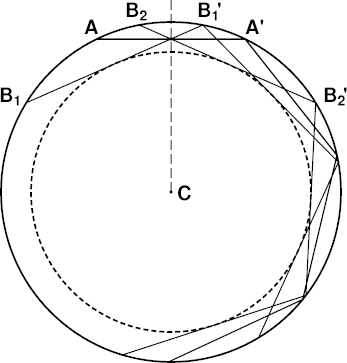observer's horizon and limiting rays in Weg. model Here's what you get when you do that. In the figure at the right, the observer is at the intersection of all the straight lines, at the midpoint of the horizon ray AA′. The two limiting rays that define Wegener's blank strip are B₁B₁′ and B₂B₂′; the B₁ ray is at the top of the blank strip, and the B₂ ray is at its lower edge, if the observer looks to our right. (Already, with just these two limiting rays, you can see why Wegener described the bottom of the duct as the envelope of the limiting rays.)

It's obvious in these last two diagrams that the period — i.e., the interval between reflections at the discontinuity — of a ducted ray depends on the ray's perigee height: the lower the perigee, the longer the period. As the limiting ray BB′… is the lowest possible ducted ray, it has the longest inter-reflection period.

So an observer's horizon ray always has a shorter period than the limiting rays. This shorter period makes successive reflections of the horizon ray steadily fall behind, relative to the limiting rays — and this mis-match between the horizon and limiting rays produces an increasing distortion of the miraged image, as Wegener noted.

Furthermore, the perigee height of an observer's horizon ray is just the observer's own height (see AA′…). But, while observers at different heights have different horizon rays, all observers have the same limiting rays, at the edges of the blank strip; it's just the phasing (rotation about C) of the limiting rays, not their shape, that changes with observer height. So, the higher the observer is above the bottom of the duct, the shorter the period of the horizon ray, and the bigger the difference between the periods of the horizon ray and the limiting rays. That makes the distortions larger for an observer nearer the top of the duct.

To put this another way: the closer the observer is to the top of the duct, the bigger are the distortions produced by the periodicity effect.

Curved rays

As long as the curvature of rays below the density discontinuity is less than the Earth's curvature, all the arguments offered above remain valid. And, as Wegener showed, the distortion in the superior mirage depends on the difference in the periods of the horizon and limiting rays; so, just as with straight rays, the distortions are larger, the closer the observer is to the discontinuity.

This is exactly what we see in the simulations. The complexity of the miraged image grows with the number of reflections of the horizon ray. So for an observer near the bottom of the duct, the mirage is a simple inverted image for nearby objects, and gradually becomes distorted and multiple for distant ones. For an observer near the top of the duct, the period discrepancy is large; so the complex images appear at shorter distances.

Realistic models

But do any of these phenomena still occur when we use a more realistic model atmosphere, instead of Wegener's impossible density discontinuity? Even when the duct is produced by an inversion of finite thickness, there is always a part of the duct below the base of the inversion. In this lower region, Wegener's periodicity effect still occurs.

Of course, in the real atmosphere, we have to replace Wegener's “reflections” with a continuous bending back down of the rays within the inversion. So the period-discrepancy effect is more complicated for an observer inside the inversion. However, for observers between the base of the inversion and the bottom of the duct, the effects predicted by Wegener, and discussed here, are still observed.

A particularly important consequence of the periodicity effect is that, as the rays at the center of the miraging zone at the astronomical horizon get increasingly out of step with those at the edges, additional transitions between inverted and erect images begin to appear in the mirage, when the target is sufficiently far away. Thus, multiple alternations of erect and inverted zones — a hallmark of the Fata Morgana — are produced, even if there is only a single inversion. The observer simply needs to be quite close beneath it.

The persistence of these properties of Wegener's simple model in realistic situations makes Wegener's periodicity effect a useful tool in understanding superior mirages, particularly those that are spectacularly complex.

Back to the . . .
introduction to Wegener's superior-mirage model

or the introduction to mirage simulations

or the main mirage page

or the GF home page

or the website overview page