Wegener's Mirage Model
Wegener's model
The simplest model for superior mirages is
Alfred Wegener's
model, as elaborated in his
1918 paper.
It reduces the inversion layer to a temperature discontinuity.
Of course, this is
completely
unphysical;
still, it captures some basic
behavior, so it's useful heuristically. Just remember that this
involves an incorrect notion: that the mirage is produced by total
internal reflection.
I'll translate a little of what Wegener says about his model into English:
A mirage can first appear if the angle of incidence exceeds the limiting
value for total reflection. Then, as seen by the observer, the mirage
must be restricted to a
strip
of definite width, whose center lies exactly in the astronomical horizon.
He then points out that the limiting value of the incidence angle
restricts all ducted rays to a spherical shell concentric with the
surfaces of constant density (or temperature) in the atmosphere.
Now comes the section of interest to us here:
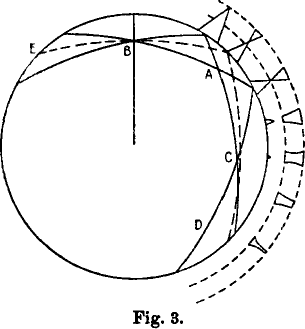 Some things about the influence of distance on the form of the
reflected images can be obtained from Fig. 3. In it are drawn the two
limiting rays of total reflection and the horizontal ray (the latter dashed)
from the observer at B. If one calculates the backward extensions to E,
the two limiting rays are obviously equally long; but the horizontal ray
is shorter.
Some things about the influence of distance on the form of the
reflected images can be obtained from Fig. 3. In it are drawn the two
limiting rays of total reflection and the horizontal ray (the latter dashed)
from the observer at B. If one calculates the backward extensions to E,
the two limiting rays are obviously equally long; but the horizontal ray
is shorter.
Consequently, the two points of reflection of the limiting rays at E, A
and D must also always be equally far apart, while the reflection point of
the horizontal ray is shifted back more at each new reflection. The path
of the rays is therefore not exactly symmetric at the reflection point A,
and at C only the two limiting rays intersect, while the horizontal ray
here runs somewhat above this intersection. But still symmetry is
preserved enough that all totally reflected rays, which fill an
appreciable space at A, are drawn together at C like a knot. Thus BC is
that distance at which the object has the greatest vertical exaggeration;
for an object of small height that is found here fills the whole width of
the reflecting strip for the observer. On the other hand, the least
distortion of the mirror image is to be expected just beyond A, reckoned
from the observer. Also, between C and D the distortion decreases again;
though it still persists here in the upper part of the mirror image up to
the reflection point. In the figure, the direct and reflected images are
schematically explained for the example of a steep pyramid: While the
erect image sinks more and more below the horizon with increasing distance
from the observer, the mirror images are bound to the totally reflecting
strip, which always lies at the same height. The reflection first
begins in the upper part of this strip; with increasing distance the
mirror image extends downward, so that the peak of the pyramid finally
would lie below the reflecting strip and is therefore invisible.
At the maximal phase of vertical distortion, occurring at C, an
interesting phenomenon now appears: beyond it, the mirror image
appears erect again. Thus the vertical distortion produces a continual
transition from inverted to erect mirror images. Thereby the presence
of this vertical distortion, which plays so great a role in mirages,
is explained.
The diagram is a little confusing, because the circle serves double duty:
first, as the reflecting density discontinuity in the atmosphere (for the
rays drawn inside it); and second, as the surface of the Earth (for the
images of the pyramid, drawn outside it). The observer is assumed to be
high enough above the surface to see a considerable width of undistorted
images below the strip that contains the miraged images.
The miraged strip is indicated in the images outside the circle by a pair
of dashed circular arcs.
Notice that Wegener generally calls this zone a “reflecting
strip” here, rather than a
“blank
strip” — a term
he introduced later in the same paper, when discussing sunset phenomena.
If you still find Wegener's diagram uninformative, try
my attempt
to explain his ideas with simpler diagrams.
Checking Wegener's sketch
In the 90 years that have elapsed since Wegener's paper was published,
computers have made it possible to do an accurate calculation for his
model. As he made no attempt to be quantitative in drawing the figure
above, and qualifies it as schematic, the height of the observer is rather
arbitrary. Furthermore, no value is offered for the temperature jump
at his zero-thickness inversion layer; so several important parameters are
left open.
 However, it's clear from his drawing and the accompanying explanation
that his pyramidal target just reached to the height of the discontinuity
that represents the inversion. So let's try collapsing our usual 2°
inversion to a very thin layer at its top, 60 m above the ground,
and choose a triangular
target
of that same height (60 m), instead of the usual 200-m target.
As the observer must be somewhere in the duct,
let's try the 54-m height of the eye used on a
previous page.
However, it's clear from his drawing and the accompanying explanation
that his pyramidal target just reached to the height of the discontinuity
that represents the inversion. So let's try collapsing our usual 2°
inversion to a very thin layer at its top, 60 m above the ground,
and choose a triangular
target
of that same height (60 m), instead of the usual 200-m target.
As the observer must be somewhere in the duct,
let's try the 54-m height of the eye used on a
previous page.
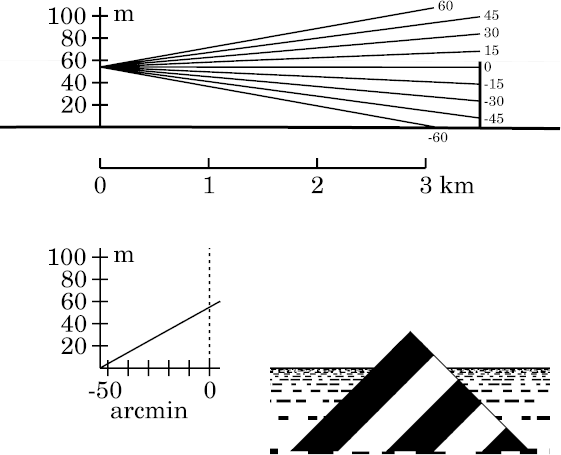
Target at 3.5 km
At the left here are the
ray diagram,
transfer curve,
and target appearance for Wegener's model when the target is 3.5 km
from the eye, which corresponds to Wegener's first drawing of his pyramid,
at the top of his
figure.
This is just inside the range at which miraging (image inversion) first appears.
The target, which (as the simulation shows) is well inside the visible
horizon, appears practically undistorted.
Note that the inversion, or discontinuity, is very dimly visible as a pale
gray line at 60 m above the surface, touching the top of the target
in the ray diagram. (As it effectively has zero thickness, there's no
gray band here marking the inversion, as there is on
the pages for more realistic models.)
Target at 10 km
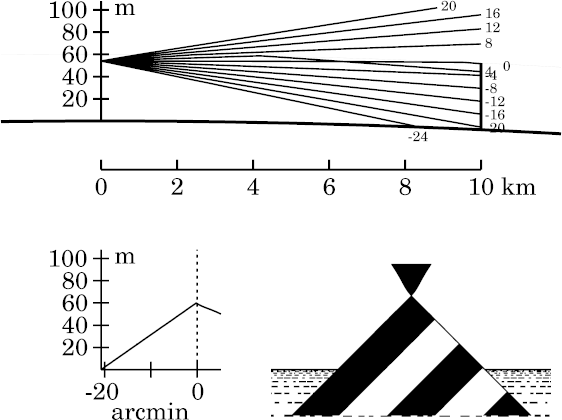 Now let's move the target out to 10 km. Here the classical superior
mirage is plainly visible; this corresponds approximately to Wegener's second
sketch, showing the miraged peak of the pyramid, in his
figure.
Now let's move the target out to 10 km. Here the classical superior
mirage is plainly visible; this corresponds approximately to Wegener's second
sketch, showing the miraged peak of the pyramid, in his
figure.
That's as Wegener predicted. But he drew the miraged point of the pyramid
with the same apex angle as that of the erect image below it —
while we see here that the miraged (reflected) image is stretched vertically:
the apex angle of the inverted image is quite acute, instead of a right
angle. That's because the reflection takes place at a concave surface,
not a flat one. And a concave mirror is a magnifying mirror — all
the more so, at grazing incidence. Wegener overlooked this magnification.
Notice that the ray at 4′ of arc above the observer's
astronomical horizon was reflected where it met the discontinuity,
a little more than 4 km from the observer.
This ray intersects the observer's horizon
ray (at 0′) between 6 and 7 km from the eye.
This ray crossing, of course, is required to produce the inverted
image of the mirage.
The corner in the transfer curve, just below the astronomical horizon,
separates the erect and inverted images. It corresponds to a ray that is
reflected by Wegener's discontinuity just at the distance of the target;
because his target is the same height as the discontinuity, that's also
the image of the target's peak.
The slopes of the two segments of the transfer curve are inversely
proportional to the magnifications of the two parts of the image: the segment
with negative slope corresponds to the inverted part of the image.
(Notice that the horizon ray is reflected just before the target; so it
belongs to the inverted part of the image.)
Target at 16 km
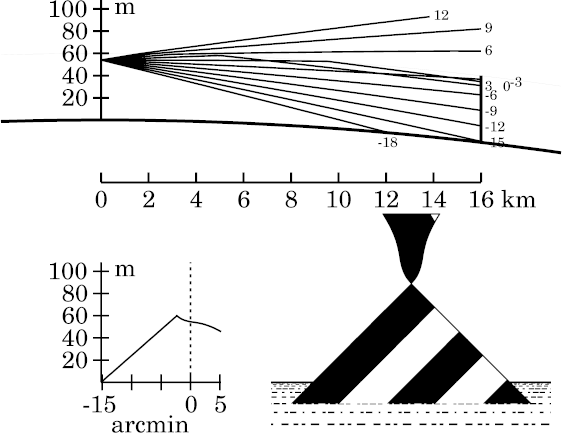 With increasing distance, another effect predicted by Wegener appears:
the distortion of the reflected (inverted) image. However, we find that
it's a bit more complicated than he indicated in his
figure.
With increasing distance, another effect predicted by Wegener appears:
the distortion of the reflected (inverted) image. However, we find that
it's a bit more complicated than he indicated in his
figure.
Here, at 16 km distance, the inverted image of the simple superior mirage
is becoming vase-shaped. That's because the magnification of the image
varies with distance. The transfer curve shows that the magnification is
greatest near the astronomical horizon; that produces the stretching in
the middle part of the vase.
Of course, this effect can be traced directly to Wegener's rule
that the observer's line of sight meets the reflecting surface overhead
at the maximum angle of incidence at the astronomical horizon.
(That maximizes the foreshortening, and hence the magnifying power, of the
concave reflector.)
The
symmetry
of that maximum explains the symmetry of the “reflecting
strip” about the astronomical horizon. (This effect is discussed
further on
another page,
in connection with Cassini's refraction model.)
The flat top on the vase here, like the flat top on the inverted image in
the
previous figure,
is the upper edge of Wegener's
strip.
(Its lower edge isn't visible at this target distance.)
The corner in the transfer curve that separates the erect and inverted
images is more than 3′ below the astronomical horizon here.
Because of the distortion of the inverted part, this corner is now a cusp.
(As before, it marks a ray that meets Wegener's discontinuity at the
target distance, and so is the image of the top of his target.)
Despite the distortion of the inverted image, we still have just two
images of the miraged parts of the target. So this would be a 2-image
superior mirage.
Target at 22 km
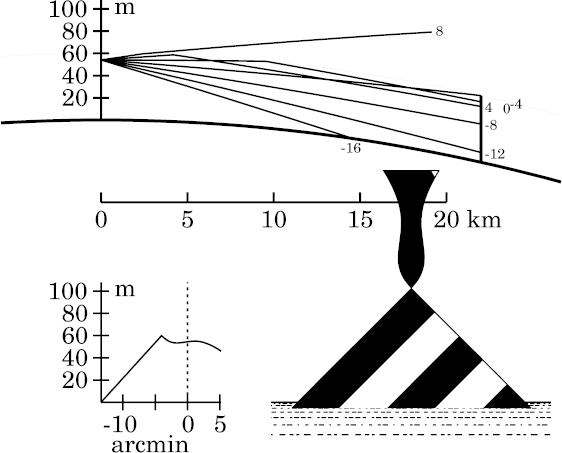 At 22 km, the “vase” has developed a waist, and resembles a
dart. The part between the waist and the bulge below it is,
of course, a vertically magnified, erect image of a small piece
of the target, near its top.
At 22 km, the “vase” has developed a waist, and resembles a
dart. The part between the waist and the bulge below it is,
of course, a vertically magnified, erect image of a small piece
of the target, near its top.
This erect image, as predicted by Wegener in discussing his
figure,
is caused by the confluence of ducted rays “like a knot”,
between 15 and 20 km from the observer.
Here, all the rays within 4′ of the observer's astronomical horizon
are roughly focused into a small part of the target; so that small part
appears expanded vertically to fill this 8′ interval.
The parts of the target that are optically conjugate to the observer's
eye are infinitely stretched, producing vertical edges in the miraged image
about 2′ above and below the astronomical horizon.
But the parts of the target less than 2′ from the
astronomical horizon lie beyond their corresponding ray-crossings (about
20 km from the observer). This ray-crossing alone would make the observer
see a real, inverted image of those parts; but that inverted image is
inverted once again by the reflection of these rays at Wegener's density
discontinuity about 10 km from the observer, producing another
ray-crossing, and hence an erect image.
As you would expect (cf. the transfer curve), this erect part of
the image is centered on the observer's astronomical horizon.
The smooth transitions here between erect and inverted sections
of the mirage are best thought of as examples of
image-folding.
Notice that these folds in the image are smooth, even though the
temperature profile was discontinuous at 60 m height. The smoothness
results from the continuous change in ray length as we look farther from
the astronomical horizon; this shifts the image inversion that occurs at
the ray-crossing smoothly through the position of the target.
The infinite vertical magnification at the image folds, and the generally
great vertical magnification of the miraged part of this image, suggest
how the Fata Morgana is formed. (Notice that the parts of the target
in the erect image near the astronomical horizon are imaged four
times here.)
The cusp in the transfer curve again marks the ray that meets Wegener's
discontinuity (at the top of the target) at the target distance: cf. the
−4′ ray in the ray diagram.
Target at 30 km
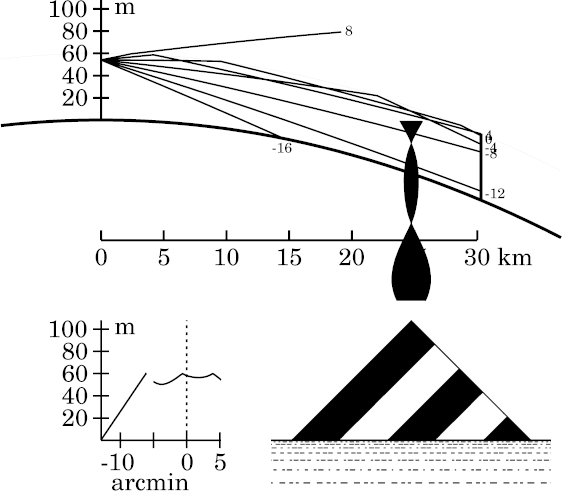 If we move the target still farther away, the lower edge of Wegener's strip
finally truncates the inverted tip of the miraged pyramid, leaving a gap
between the inverted superior mirage and the direct image below it,
as he
predicted,
The lower edge of the strip can be regarded as a superior mirage of the
upper edge.
If we move the target still farther away, the lower edge of Wegener's strip
finally truncates the inverted tip of the miraged pyramid, leaving a gap
between the inverted superior mirage and the direct image below it,
as he
predicted,
The lower edge of the strip can be regarded as a superior mirage of the
upper edge.
Here, the full width of the miraging strip is visible — from about
5′ above the astronomical horizon to 5′ below it (see the
transfer curve).
The transfer curve now has two cusps. Each marks a double image
(erect and inverted) of the top of the target. The cusp at 4′ above
the astronomical horizon corresponds to a ray reflected at Wegener's
discontinuity about 4 km from the observer; it just reaches the
discontinuity (and hence the top of Wegener's target) again at the target.
The second cusp, just below the astronomical horizon, corresponds to a ray
reflected twice: once about 10 km from the observer, and then again
a few km before the target. (This ray is not shown; but the ray at the
astronomical horizon gives a good idea of where it goes.)
This double reflection illustrates Wegener's
discussion
of the relative intervals between reflections of rays at the horizon and at
the edges of the miraged strip. Rays near the astronomical horizon are
reflected at shorter intervals than rays near the edges of the strip,
so there is room for two reflections of rays near the horizon between
observer and target, but only one for rays with greater inclinations.
(I have a more detailed discussion of this principle on
another page.)
Furthermore, as reflections at Wegener's discontinuity alternate with
ray-crossings between reflections, and both produce image inversions,
we see that the number of image inversions increases from the edges of the
strip (which have only a single inversion, and hence an inverted image)
to its center. So we see two inversions, and hence an erect image, near
altitudes of ±3 ′; but 3 inversions (an inverted image again)
at the astronomical horizon itself (just above the lower cusp).
Hence, we see as many as 5 or 6 images of some miraged regions.
These multiple images would easily be visible to the naked eye.
This suggests that the Fata Morgana is simply a superior mirage of a
sufficiently distant object. In terms of Wegener's simple reflections,
it requires multiple reflections of the rays at the top of the duct.
Wegener's
insight
into the relation between the interval between
successive reflections along different rays and the distortions in
superior mirages is also useful for understanding the effect of eye
height
on these mirages.
Final remarks
Wegener's “toy” mirage model already shows more complex
behavior than he had expected. However, it's too unrealistic to be used
to interpret actual superior-mirage displays. To understand the real
world, we need to use a
more realistic model
of the inversion to generate the simulations.
Copyright © 2008 – 2009, 2012 Andrew T. Young
Back to the . . .
introduction to superior-mirage simulations
or the
introduction to all mirage simulations
or the
main mirage page
or the
GF home page
or the
website overview page
 Some things about the influence of distance on the form of the
reflected images can be obtained from Fig. 3. In it are drawn the two
limiting rays of total reflection and the horizontal ray (the latter dashed)
from the observer at B. If one calculates the backward extensions to E,
the two limiting rays are obviously equally long; but the horizontal ray
is shorter.
Some things about the influence of distance on the form of the
reflected images can be obtained from Fig. 3. In it are drawn the two
limiting rays of total reflection and the horizontal ray (the latter dashed)
from the observer at B. If one calculates the backward extensions to E,
the two limiting rays are obviously equally long; but the horizontal ray
is shorter.
 However, it's clear from his drawing and the accompanying explanation
that his pyramidal target just reached to the height of the discontinuity
that represents the inversion. So let's try collapsing our usual 2°
inversion to a very thin layer at its top, 60 m above the ground,
and choose a triangular
However, it's clear from his drawing and the accompanying explanation
that his pyramidal target just reached to the height of the discontinuity
that represents the inversion. So let's try collapsing our usual 2°
inversion to a very thin layer at its top, 60 m above the ground,
and choose a triangular
 Now let's move the target out to 10 km. Here the classical superior
mirage is plainly visible; this corresponds approximately to Wegener's second
sketch, showing the miraged peak of the pyramid, in his
figure.
Now let's move the target out to 10 km. Here the classical superior
mirage is plainly visible; this corresponds approximately to Wegener's second
sketch, showing the miraged peak of the pyramid, in his
figure.
 With increasing distance, another effect predicted by Wegener appears:
the distortion of the reflected (inverted) image. However, we find that
it's a bit more complicated than he indicated in his
figure.
With increasing distance, another effect predicted by Wegener appears:
the distortion of the reflected (inverted) image. However, we find that
it's a bit more complicated than he indicated in his
figure.
 At 22 km, the “vase” has developed a waist, and resembles a
dart. The part between the waist and the bulge below it is,
of course, a vertically magnified, erect image of a small piece
of the target, near its top.
At 22 km, the “vase” has developed a waist, and resembles a
dart. The part between the waist and the bulge below it is,
of course, a vertically magnified, erect image of a small piece
of the target, near its top.
 If we move the target still farther away, the lower edge of Wegener's strip
finally truncates the inverted tip of the miraged pyramid, leaving a gap
between the inverted superior mirage and the direct image below it,
as he
predicted,
The lower edge of the strip can be regarded as a superior mirage of the
upper edge.
If we move the target still farther away, the lower edge of Wegener's strip
finally truncates the inverted tip of the miraged pyramid, leaving a gap
between the inverted superior mirage and the direct image below it,
as he
predicted,
The lower edge of the strip can be regarded as a superior mirage of the
upper edge.