However, there are some simple optical principles that may help you put things in perspective. This page tries to do that.
In mirages, the commonest wrong notion is that mirages are caused by total internal reflection: light incident on the boundary between “denser” (to use an antiquated term that is still with us) and “less dense” media at near-grazing angles from the denser side cannot penetrate into the less-dense medium, because the sine law of refraction would require the sine of the angle of refraction to be greater than unity — an impossibility for real angles. As the light cannot be refracted at the boundary and enter the less-dense material, it's totally reflected back into the denser medium. In the incorrect explanation of mirages, the warmer air plays the part of the less-dense medium. (Well, the warmer air is certainly less dense, both mechanically and optically; but that doesn't make the internal-reflection argument correct.)
Historically, it's not helpful that the French physicist Gaspard Monge originally explained the inferior mirage in terms of total internal reflection, nor that the very word mirage (which Monge borrowed from French sailors, and William Wollaston then adopted into English from Monge's work) is derived from a phrase meaning “to be reflected”. This folly is still promoted by physicists who try to invoke mirages as an everyday example of total internal reflection.
Monge's internal-reflection model was justly criticized by Everett (1874). While some forms of mirage can qualitatively be explained in these terms (though only in the limited sense that an inverted image can be produced by reflection at a level surface), the quantitative explanation of details such as magnification, distortion, and the smooth folding-over of images where the erect and inverted ones come together — not to mention phenomena like the mock mirage and Wegener's Nachspiegelung, which “internal reflection” cannot begin to suggest — can only be done in terms of refraction.
Finally, heat transfer in the actual atmosphere makes the density discontinuities used in the simple internal-reflection argument impossible. So the model on which the reflection argument rests is physically wrong.
A more correct view is that, while both total internal reflection and inferior mirages are consequences of the sine law, the lack of propagation of rays into the less-dense air in mirages is better explained in terms of another of its consequences: the refractive invariant. But this emphasizes the refractive nature of mirages.
The basic effect of a prism is to deviate a beam of light. If you look at the bending page, you'll see that the curvature of a nearly-horizontal beam of light is proportional to the local density gradient in the atmosphere. A constant gradient means a steady bending of the light; the atmosphere acts like a distributed prism, or a succession of little thin prisms, evenly spaced, so that the overall effect is like one thicker prism.
What makes a constant density gradient? The density of air is directly proportional to its pressure. And, as we're usually interested in layers just a few tens of meters thick (i.e., less than 1% of the effective thickness of the atmosphere), the pressure variation required by hydrostatic equilibrium can be regarded as linear over this thin region. A linear variation means a constant gradient ; so the change of pressure with height produces a constant density gradient in the air.
Likewise, though the air's density is inversely proportional to its temperature, the change of a few degrees in the region where mirages are produced is only a few per cent of the total; so once again, a constant temperature gradient (i.e., a constant lapse rate , to use the meteorologists' term) produces a nearly linear change in density with height: a constant density gradient . So the sum of these two constant density gradients — one due to the pressure gradient, and the other due to the temperature gradient — is itself a constant gradient. The atmosphere acts like a prism IF the lapse rate is constant.
Sure enough, Lambert showed in 1759 that a constant temperature variation in the vertical direction would only produce displacements of objects, not distortions and inversions. He thought he had proved that early reports of mirages were impossible; but he only showed that mirages are impossible when the lapse rate is constant.
Obviously, what's needed to produce all the interesting phenomena of mirages is a variation in the lapse rate. So let's look at a lapse rate that changes with height. As the lapse rate is (in terms of elementary calculus) the first derivative of the temperature profile, we need to look at the second derivative: the curvature of the temperature profile.
But it isn't immediately obvious that the atmosphere acts like a lens, primarily because the density usually decreases steadily from the ground up. We're used to thinking of lenses that are symmetrical, with either a maximum or minimum of optical path in the middle.
But if you think of subtracting out the average density gradient, what's left is (to lowest order) a parabolic variation. The average gradient acts like a prism; so an atmosphere with a gradual change in the lapse rate acts like the sum of a prism (due to the average gradient) and a lens. Subtract the prism from the sum, and you're left with the lens-like part. The lensing effect was discussed by Everett (1873).
To be sure, the atmospheric lens isn't the rotationally-symmetrical lens of a camera. The atmosphere has great astigmatism — a fact that was discussed at length in Friedrich Dobe's thesis, though only for a constant-lapse-rate model like the Standard Atmosphere. Dobe found that the image formed in the vertical plane would be 500 km behind the observer, because of the weakness of the higher-order terms that we neglected in the discussion above. The focusing power of the normal atmosphere is a thousand times weaker yet in the horizontal plane, according to Dobe; if we neglect it completely, the atmosphere is a cylindrical lens, with the axis of the cylinder parallel to the horizon.
However, when rapid changes in lapse rate occur, the focal length of the atmospheric lens can be less than a kilometer. When strong mirage effects are present, the focal length can even be a few centimeters. One often finds that the astigmatic image is formed very close to the hot surface in inferior mirages, especially if a telephoto lens or a pair of binoculars is used to examine them. Indeed, the astigmatism sometimes makes the miraged image impossible to focus on and recognize in such cases.
Enough of these generalities; let's look at some specific examples.
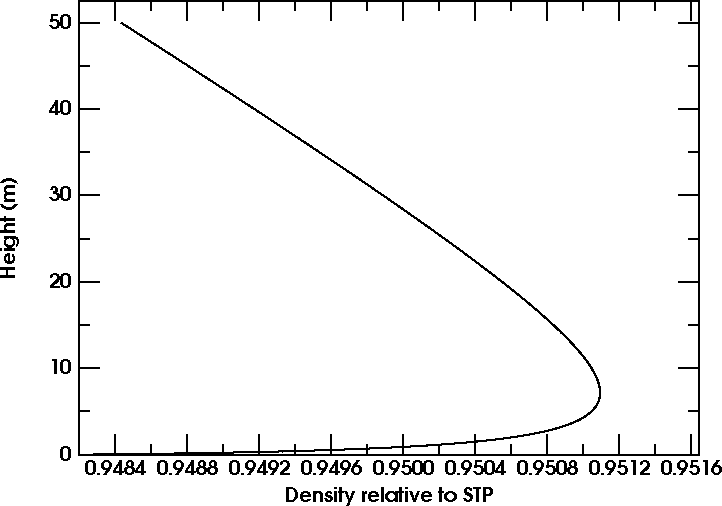Here's the run of density in the lowest 50 meters of the
model atmosphere
used for most of my inferior-mirage calculations. You can see that
a maximum occurs at about 7 m above the sea surface.
The maximum in itself is insignificant. What's important here is that the whole run of density in the region where the inferior mirage is formed is convex to the right: that is, if you draw a chord between any two points on the curve, the part of the curve between them lies to the right of the chord. That chord represents the prism part of that layer in the atmosphere; the bulge of the curve to the right of the chord represents the lens part, which acts like a positive (converging) lens.
The lens-like effect of this strongly curved density profile means that the atmospheric focal length is much shorter here than in Dobe's simpler atmosphere. The curvature of the profile increases steadily downwards, and is greatest at the warm surface, so that the focal length in the lowest few meters is on the order of a kilometer. That means that the atmospheric lens can form a real, inverted image (in the vertical plane only, of course) of objects just a few km away. And, in fact, the simulations of inferior mirages show exactly that: inverted images of objects just beyond the horizon for an observer standing at the shoreline.
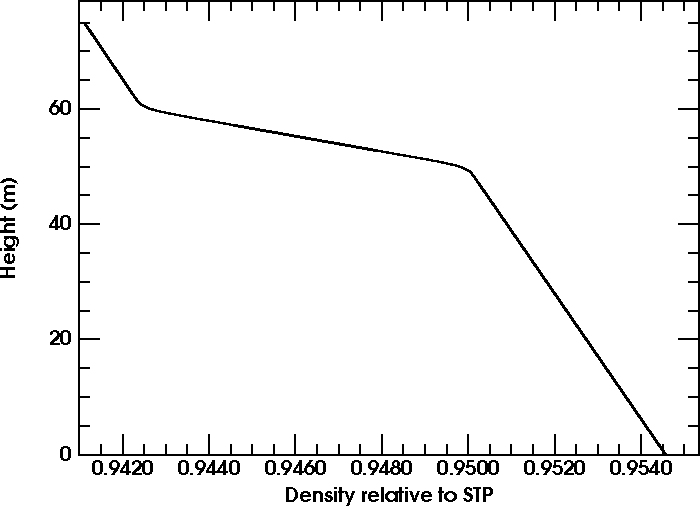Similarly, here's the density plot for the lowest 75m of the
duct model
I've used for several simulations; it has a 2° thermal inversion between
50 and 60 m height, smoothed at the edges to represent the effects of
heat transfer.
Both the
mock mirage
and the
3-image form of the
superior mirage
are produced at its lower edge, near 50 m. (An observer above
50 m sees a mock mirage there; someone just below that height can see
a 3-image mirage. Click on the links in the previous sentence to see
simulations of these mirages.)
Notice that all these different mirages have one thing in common: a density profile with a rounded corner that's convex to the right, so that it acts like a converging lens. And that corner is where the lapse rate decreases with increasing height. Also, notice that the duct — unlike the inferior-mirage profile — doesn't have an actual density maximum. It just has a smooth bend in the right direction.
Copyright © 2008 – 2012, 2025 Andrew T. Young
or the
introduction to mirage simulations
or the
GF home page
or the website overview page